Reevu Maity
Learning Unitaries by Gradient Descent
Feb 18, 2020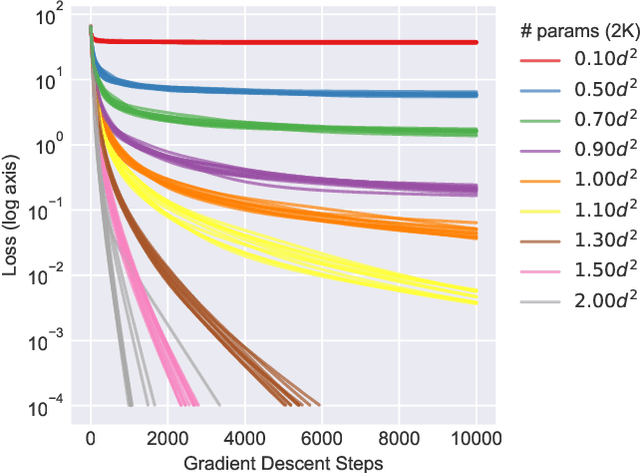
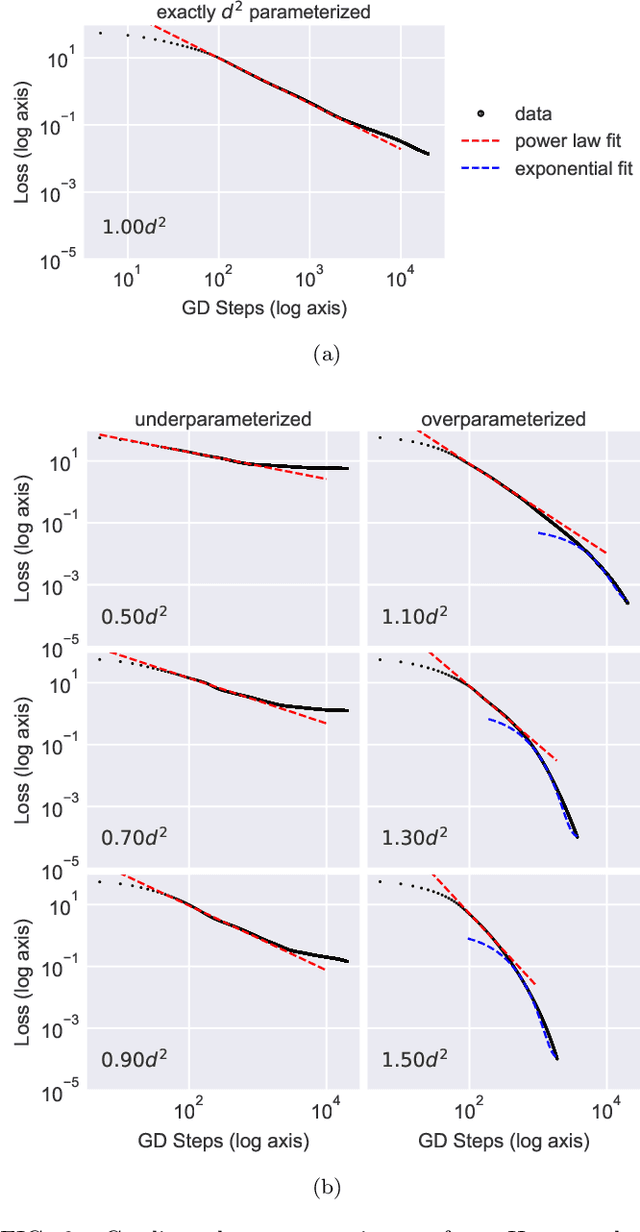
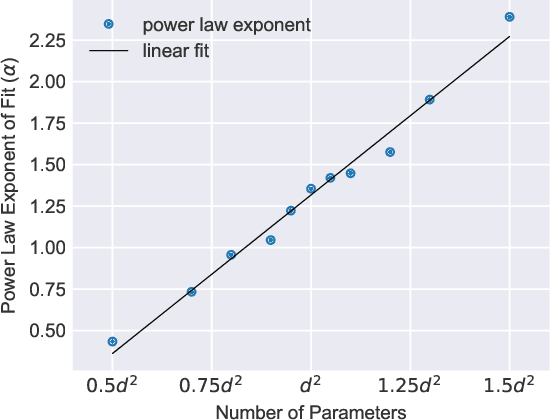
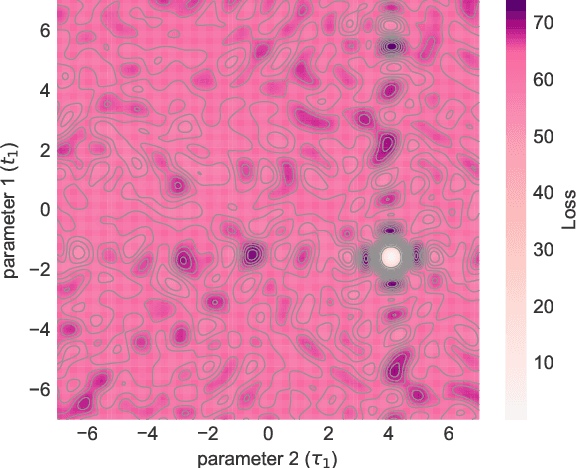
Abstract:We study the hardness of learning unitary transformations in $U(d)$ via gradient descent on time parameters of alternating operator sequences. We provide numerical evidence that, despite the non-convex nature of the loss landscape, gradient descent always converges to the target unitary when the sequence contains $d^2$ or more parameters. Rates of convergence indicate a "computational phase transition." With less than $d^2$ parameters, gradient descent converges to a sub-optimal solution, whereas with more than $d^2$ parameters, gradient descent converges exponentially to an optimal solution.
Quantum Boosting
Feb 12, 2020Abstract:Suppose we have a weak learning algorithm $\mathcal{A}$ for a Boolean-valued problem: $\mathcal{A}$ produces hypotheses whose bias $\gamma$ is small, only slightly better than random guessing (this could, for instance, be due to implementing $\mathcal{A}$ on a noisy device), can we boost the performance of $\mathcal{A}$ so that $\mathcal{A}$'s output is correct on $2/3$ of the inputs? Boosting is a technique that converts a weak and inaccurate machine learning algorithm into a strong accurate learning algorithm. The AdaBoost algorithm by Freund and Schapire (for which they were awarded the G\"odel prize in 2003) is one of the widely used boosting algorithms, with many applications in theory and practice. Suppose we have a $\gamma$-weak learner for a Boolean concept class $C$ that takes time $R(C)$, then the time complexity of AdaBoost scales as $VC(C)\cdot poly(R(C), 1/\gamma)$, where $VC(C)$ is the $VC$-dimension of $C$. In this paper, we show how quantum techniques can improve the time complexity of classical AdaBoost. To this end, suppose we have a $\gamma$-weak quantum learner for a Boolean concept class $C$ that takes time $Q(C)$, we introduce a quantum boosting algorithm whose complexity scales as $\sqrt{VC(C)}\cdot poly(Q(C),1/\gamma);$ thereby achieving a quadratic quantum improvement over classical AdaBoost in terms of $VC(C)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge