Exploring Maximum Entropy Distributions with Evolutionary Algorithms

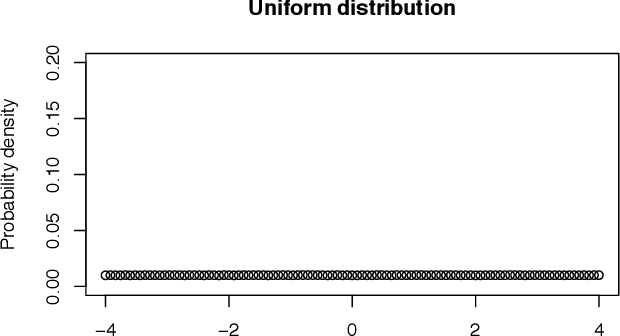
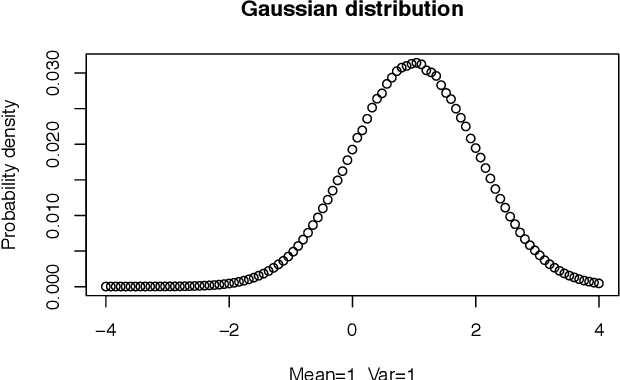
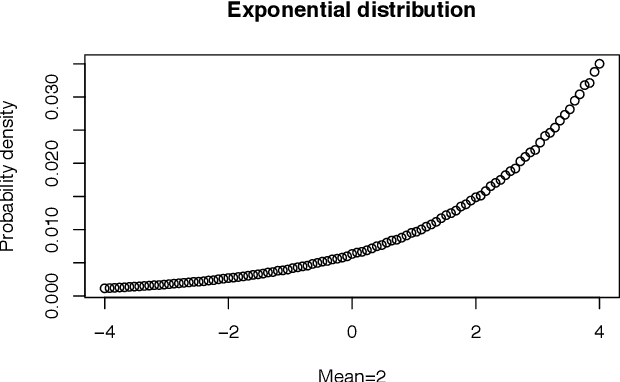
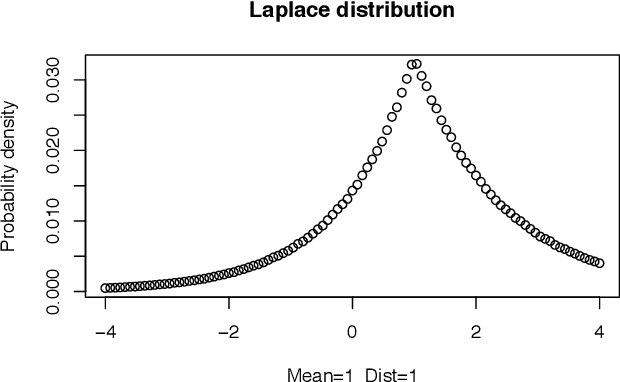
This paper shows how to evolve numerically the maximum entropy probability distributions for a given set of constraints, which is a variational calculus problem. An evolutionary algorithm can obtain approximations to some well-known analytical results, but is even more flexible and can find distributions for which a closed formula cannot be readily stated. The numerical approach handles distributions over finite intervals. We show that there are two ways of conducting the procedure: by direct optimization of the Lagrangian of the constrained problem, or by optimizing the entropy among the subset of distributions which fulfill the constraints. An incremental evolutionary strategy easily obtains the uniform, the exponential, the Gaussian, the log-normal, the Laplace, among other distributions, once the constrained problem is solved with any of the two methods. Solutions for mixed ("chimera") distributions can be also found. We explain why many of the distributions are symmetrical and continuous, but some are not.

Logistic Regression as Soft Perceptron Learning

We comment on the fact that gradient ascent for logistic regression has a connection with the perceptron learning algorithm. Logistic learning is the "soft" variant of perceptron learning.

Deepest Neural Networks

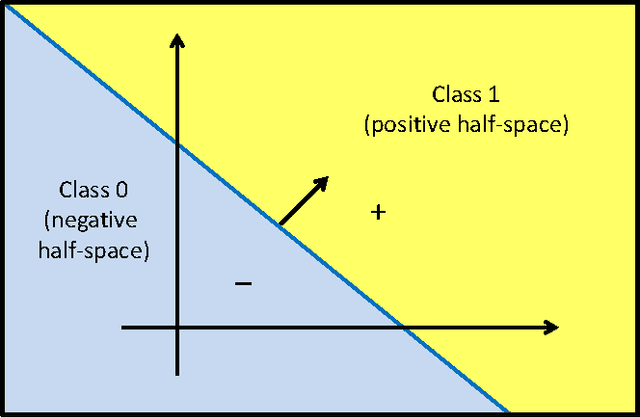
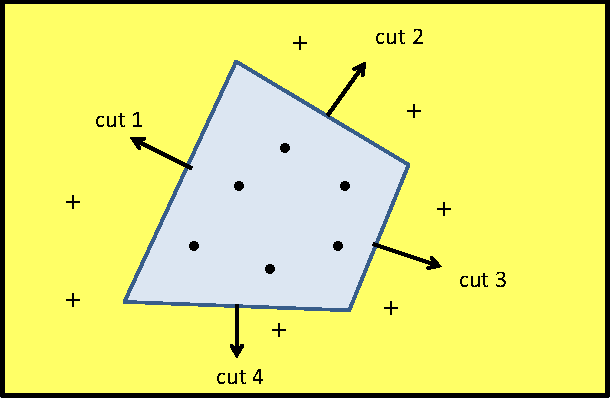
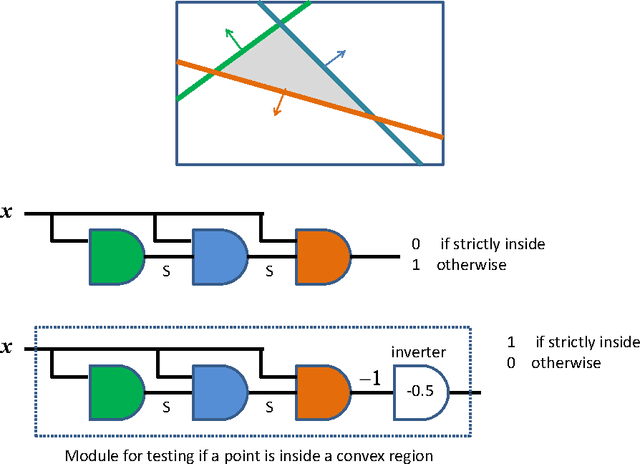
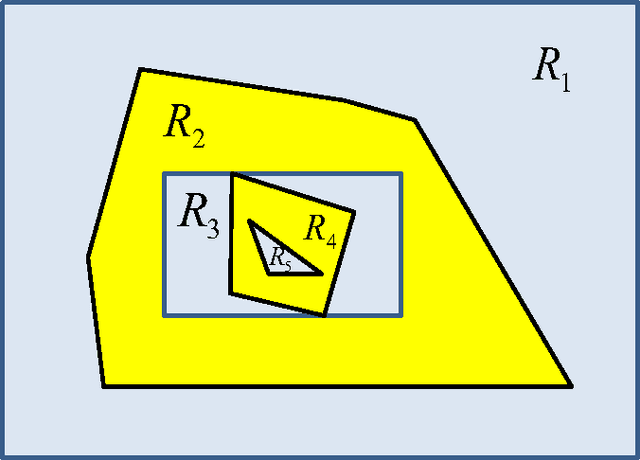
This paper shows that a long chain of perceptrons (that is, a multilayer perceptron, or MLP, with many hidden layers of width one) can be a universal classifier. The classification procedure is not necessarily computationally efficient, but the technique throws some light on the kind of computations possible with narrow and deep MLPs.