Creator Incentives in Recommender Systems: A Cooperative Game-Theoretic Approach for Stable and Fair Collaboration in Multi-Agent Bandits

User interactions in online recommendation platforms create interdependencies among content creators: feedback on one creator's content influences the system's learning and, in turn, the exposure of other creators' contents. To analyze incentives in such settings, we model collaboration as a multi-agent stochastic linear bandit problem with a transferable utility (TU) cooperative game formulation, where a coalition's value equals the negative sum of its members' cumulative regrets. We show that, for identical (homogenous) agents with fixed action sets, the induced TU game is convex under mild algorithmic conditions, implying a non-empty core that contains the Shapley value and ensures both stability and fairness. For heterogeneous agents, the game still admits a non-empty core, though convexity and Shapley value core-membership are no longer guaranteed. To address this, we propose a simple regret-based payout rule that satisfies three out of the four Shapley axioms and also lies in the core. Experiments on MovieLens-100k dataset illustrate when the empirical payout aligns with -- and diverges from -- the Shapley fairness across different settings and algorithms.

On Slowly-varying Non-stationary Bandits

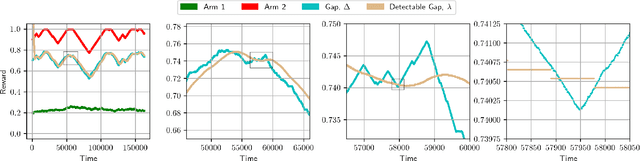
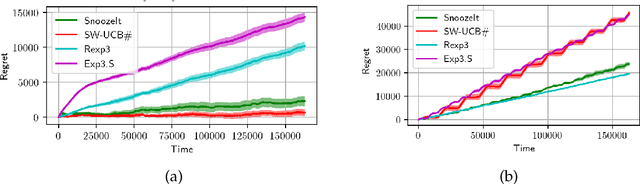
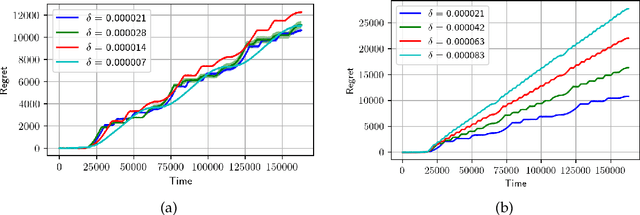
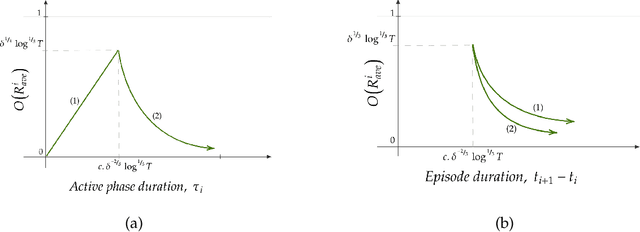
We consider minimisation of dynamic regret in non-stationary bandits with a slowly varying property. Namely, we assume that arms' rewards are stochastic and independent over time, but that the absolute difference between the expected rewards of any arm at any two consecutive time-steps is at most a drift limit $\delta > 0$. For this setting that has not received enough attention in the past, we give a new algorithm which extends naturally the well-known Successive Elimination algorithm to the non-stationary bandit setting. We establish the first instance-dependent regret upper bound for slowly varying non-stationary bandits. The analysis in turn relies on a novel characterization of the instance as a detectable gap profile that depends on the expected arm reward differences. We also provide the first minimax regret lower bound for this problem, enabling us to show that our algorithm is essentially minimax optimal. Also, this lower bound we obtain matches that of the more general total variation-budgeted bandits problem, establishing that the seemingly easier former problem is at least as hard as the more general latter problem in the minimax sense. We complement our theoretical results with experimental illustrations.

Optimal Algorithms for Range Searching over Multi-Armed Bandits

This paper studies a multi-armed bandit (MAB) version of the range-searching problem. In its basic form, range searching considers as input a set of points (on the real line) and a collection of (real) intervals. Here, with each specified point, we have an associated weight, and the problem objective is to find a maximum-weight point within every given interval. The current work addresses range searching with stochastic weights: each point corresponds to an arm (that admits sample access) and the point's weight is the (unknown) mean of the underlying distribution. In this MAB setup, we develop sample-efficient algorithms that find, with high probability, near-optimal arms within the given intervals, i.e., we obtain PAC (probably approximately correct) guarantees. We also provide an algorithm for a generalization wherein the weight of each point is a multi-dimensional vector. The sample complexities of our algorithms depend, in particular, on the size of the optimal hitting set of the given intervals. Finally, we establish lower bounds proving that the obtained sample complexities are essentially tight. Our results highlight the significance of geometric constructs -- specifically, hitting sets -- in our MAB setting.