DIP-GS: Deep Image Prior For Gaussian Splatting Sparse View Recovery

3D Gaussian Splatting (3DGS) is a leading 3D scene reconstruction method, obtaining high-quality reconstruction with real-time rendering runtime performance. The main idea behind 3DGS is to represent the scene as a collection of 3D gaussians, while learning their parameters to fit the given views of the scene. While achieving superior performance in the presence of many views, 3DGS struggles with sparse view reconstruction, where the input views are sparse and do not fully cover the scene and have low overlaps. In this paper, we propose DIP-GS, a Deep Image Prior (DIP) 3DGS representation. By using the DIP prior, which utilizes internal structure and patterns, with coarse-to-fine manner, DIP-based 3DGS can operate in scenarios where vanilla 3DGS fails, such as sparse view recovery. Note that our approach does not use any pre-trained models such as generative models and depth estimation, but rather relies only on the input frames. Among such methods, DIP-GS obtains state-of-the-art (SOTA) competitive results on various sparse-view reconstruction tasks, demonstrating its capabilities.

TriNeRFLet: A Wavelet Based Multiscale Triplane NeRF Representation

In recent years, the neural radiance field (NeRF) model has gained popularity due to its ability to recover complex 3D scenes. Following its success, many approaches proposed different NeRF representations in order to further improve both runtime and performance. One such example is Triplane, in which NeRF is represented using three 2D feature planes. This enables easily using existing 2D neural networks in this framework, e.g., to generate the three planes. Despite its advantage, the triplane representation lagged behind in its 3D recovery quality compared to NeRF solutions. In this work, we propose TriNeRFLet, a 2D wavelet-based multiscale triplane representation for NeRF, which closes the 3D recovery performance gap and is competitive with current state-of-the-art methods. Building upon the triplane framework, we also propose a novel super-resolution (SR) technique that combines a diffusion model with TriNeRFLet for improving NeRF resolution.

Learned Greedy Method (LGM): A Novel Neural Architecture for Sparse Coding and Beyond

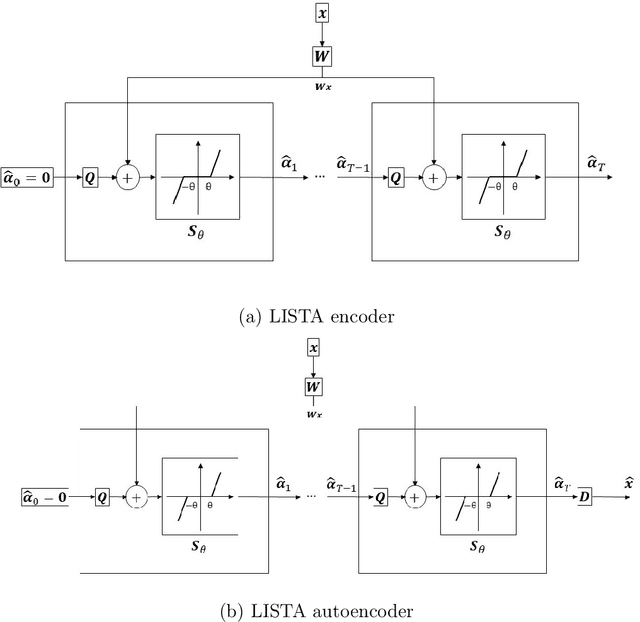
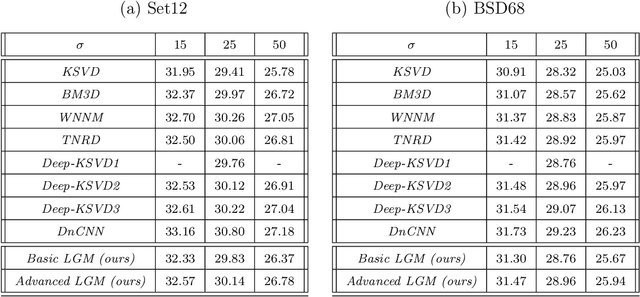
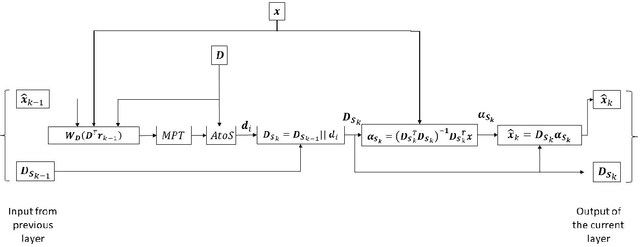
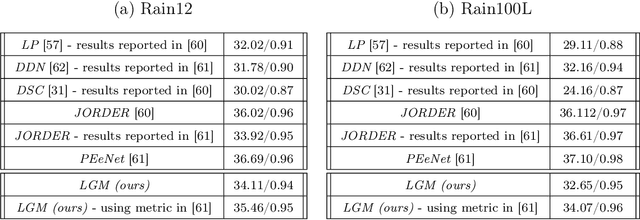
The fields of signal and image processing have been deeply influenced by the introduction of deep neural networks. These are successfully deployed in a wide range of real-world applications, obtaining state of the art results and surpassing well-known and well-established classical methods. Despite their impressive success, the architectures used in many of these neural networks come with no clear justification. As such, these are usually treated as "black box" machines that lack any kind of interpretability. A constructive remedy to this drawback is a systematic design of such networks by unfolding well-understood iterative algorithms. A popular representative of this approach is the Iterative Shrinkage-Thresholding Algorithm (ISTA) and its learned version -- LISTA, aiming for the sparse representations of the processed signals. In this paper we revisit this sparse coding task and propose an unfolded version of a greedy pursuit algorithm for the same goal. More specifically, we concentrate on the well-known Orthogonal-Matching-Pursuit (OMP) algorithm, and introduce its unfolded and learned version. Key features of our Learned Greedy Method (LGM) are the ability to accommodate a dynamic number of unfolded layers, and a stopping mechanism based on representation error, both adapted to the input. We develop several variants of the proposed LGM architecture and test some of them in various experiments, demonstrating their flexibility and efficiency.