A Multicenter Benchmark of Multiple Instance Learning Models for Lymphoma Subtyping from HE-stained Whole Slide Images

Timely and accurate lymphoma diagnosis is essential for guiding cancer treatment. Standard diagnostic practice combines hematoxylin and eosin (HE)-stained whole slide images with immunohistochemistry, flow cytometry, and molecular genetic tests to determine lymphoma subtypes, a process requiring costly equipment, skilled personnel, and causing treatment delays. Deep learning methods could assist pathologists by extracting diagnostic information from routinely available HE-stained slides, yet comprehensive benchmarks for lymphoma subtyping on multicenter data are lacking. In this work, we present the first multicenter lymphoma benchmarking dataset covering four common lymphoma subtypes and healthy control tissue. We systematically evaluate five publicly available pathology foundation models (H-optimus-1, H0-mini, Virchow2, UNI2, Titan) combined with attention-based (AB-MIL) and transformer-based (TransMIL) multiple instance learning aggregators across three magnifications (10x, 20x, 40x). On in-distribution test sets, models achieve multiclass balanced accuracies exceeding 80% across all magnifications, with all foundation models performing similarly and both aggregation methods showing comparable results. The magnification study reveals that 40x resolution is sufficient, with no performance gains from higher resolutions or cross-magnification aggregation. However, on out-of-distribution test sets, performance drops substantially to around 60%, highlighting significant generalization challenges. To advance the field, larger multicenter studies covering additional rare lymphoma subtypes are needed. We provide an automated benchmarking pipeline to facilitate such future research.

BITES: Balanced Individual Treatment Effect for Survival data

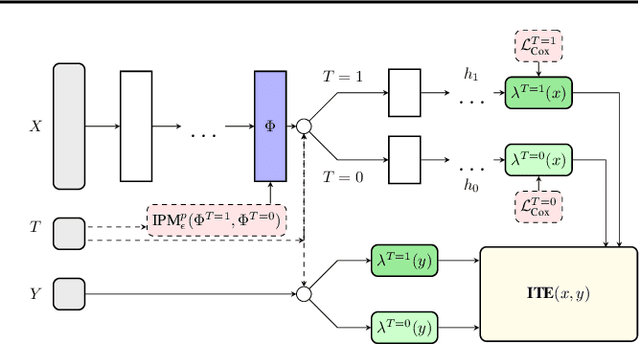
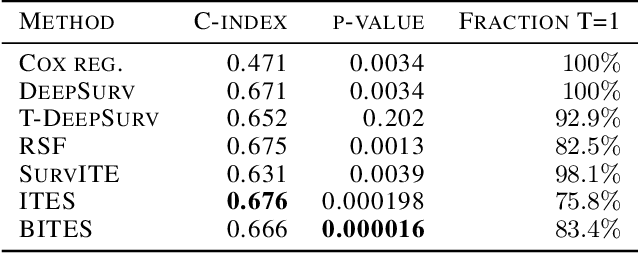
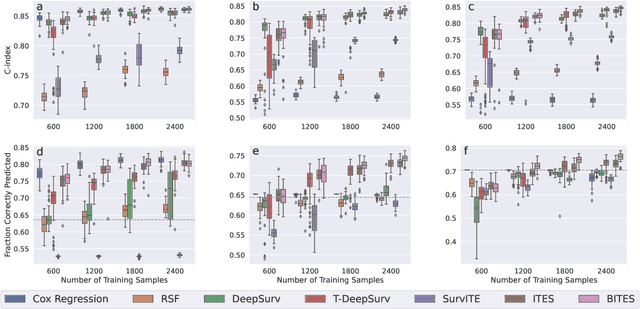
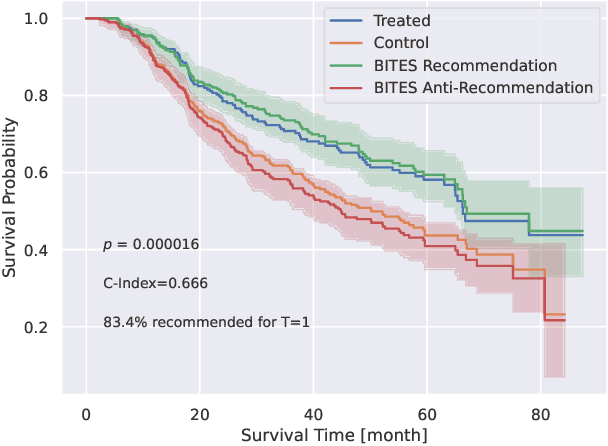
Estimating the effects of interventions on patient outcome is one of the key aspects of personalized medicine. Their inference is often challenged by the fact that the training data comprises only the outcome for the administered treatment, and not for alternative treatments (the so-called counterfactual outcomes). Several methods were suggested for this scenario based on observational data, i.e.~data where the intervention was not applied randomly, for both continuous and binary outcome variables. However, patient outcome is often recorded in terms of time-to-event data, comprising right-censored event times if an event does not occur within the observation period. Albeit their enormous importance, time-to-event data is rarely used for treatment optimization. We suggest an approach named BITES (Balanced Individual Treatment Effect for Survival data), which combines a treatment-specific semi-parametric Cox loss with a treatment-balanced deep neural network; i.e.~we regularize differences between treated and non-treated patients using Integral Probability Metrics (IPM). We show in simulation studies that this approach outperforms the state of the art. Further, we demonstrate in an application to a cohort of breast cancer patients that hormone treatment can be optimized based on six routine parameters. We successfully validated this finding in an independent cohort. BITES is provided as an easy-to-use python implementation.

Differentiated uniformization: A new method for inferring Markov chains on combinatorial state spaces including stochastic epidemic models

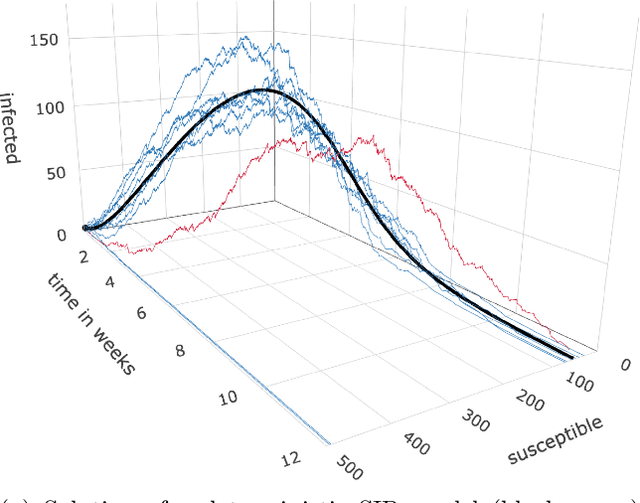
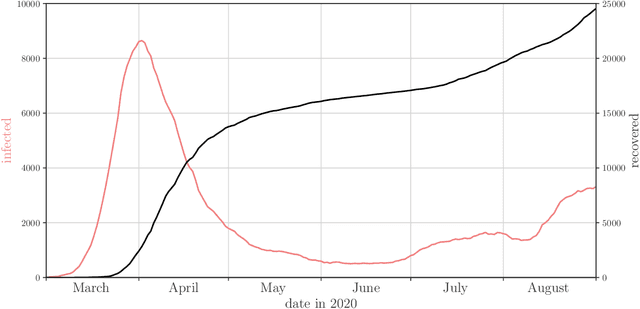
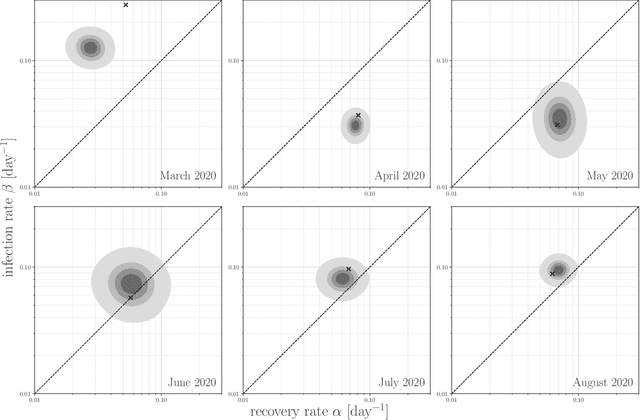
Motivation: We consider continuous-time Markov chains that describe the stochastic evolution of a dynamical system by a transition-rate matrix $Q$ which depends on a parameter $\theta$. Computing the probability distribution over states at time $t$ requires the matrix exponential $\exp(tQ)$, and inferring $\theta$ from data requires its derivative $\partial\exp\!(tQ)/\partial\theta$. Both are challenging to compute when the state space and hence the size of $Q$ is huge. This can happen when the state space consists of all combinations of the values of several interacting discrete variables. Often it is even impossible to store $Q$. However, when $Q$ can be written as a sum of tensor products, computing $\exp(tQ)$ becomes feasible by the uniformization method, which does not require explicit storage of $Q$. Results: Here we provide an analogous algorithm for computing $\partial\exp\!(tQ)/\partial\theta$, the differentiated uniformization method. We demonstrate our algorithm for the stochastic SIR model of epidemic spread, for which we show that $Q$ can be written as a sum of tensor products. We estimate monthly infection and recovery rates during the first wave of the COVID-19 pandemic in Austria and quantify their uncertainty in a full Bayesian analysis. Availability: Implementation and data are available at https://github.com/spang-lab/TenSIR.