A Quantum Approximation Scheme for k-Means

We give a quantum approximation scheme (i.e., $(1 + \varepsilon)$-approximation for every $\varepsilon > 0$) for the classical $k$-means clustering problem in the QRAM model with a running time that has only polylogarithmic dependence on the number of data points. More specifically, given a dataset $V$ with $N$ points in $\mathbb{R}^d$ stored in QRAM data structure, our quantum algorithm runs in time $\tilde{O} \left( 2^{\tilde{O}(\frac{k}{\varepsilon})} \eta^2 d\right)$ and with high probability outputs a set $C$ of $k$ centers such that $cost(V, C) \leq (1+\varepsilon) \cdot cost(V, C_{OPT})$. Here $C_{OPT}$ denotes the optimal $k$-centers, $cost(.)$ denotes the standard $k$-means cost function (i.e., the sum of the squared distance of points to the closest center), and $\eta$ is the aspect ratio (i.e., the ratio of maximum distance to minimum distance). This is the first quantum algorithm with a polylogarithmic running time that gives a provable approximation guarantee of $(1+\varepsilon)$ for the $k$-means problem. Also, unlike previous works on unsupervised learning, our quantum algorithm does not require quantum linear algebra subroutines and has a running time independent of parameters (e.g., condition number) that appear in such procedures.

Universal Weak Coreset

Coresets for $k$-means and $k$-median problems yield a small summary of the data, which preserve the clustering cost with respect to any set of $k$ centers. Recently coresets have also been constructed for constrained $k$-means and $k$-median problems. However, the notion of coresets has the drawback that (i) they can only be applied in settings where the input points are allowed to have weights, and (ii) in general metric spaces, the size of the coresets can depend logarithmically on the number of points. The notion of weak coresets, which have less stringent requirements than coresets, has been studied in the context of classical $k$-means and $k$-median problems. A weak coreset is a pair $(J,S)$ of subsets of points, where $S$ acts as a summary of the point set and $J$ as a set of potential centers. This pair satisfies the properties that (i) $S$ is a good summary of the data as long as the $k$ centers are chosen from $J$ only, and (ii) there is a good choice of $k$ centers in $J$ with cost close to the optimal cost. We develop this framework, which we call universal weak coresets, for constrained clustering settings. In conjunction with recent coreset constructions for constrained settings, our designs give greater data compression, are conceptually simpler, and apply to a wide range of constrained $k$-median and $k$-means problems.

Tight FPT Approximation for Constrained k-Center and k-Supplier

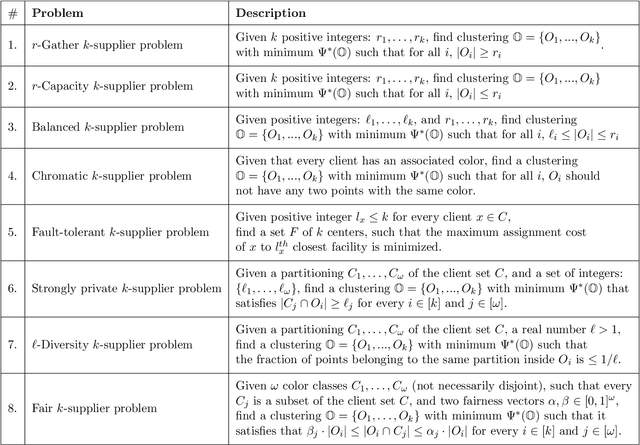
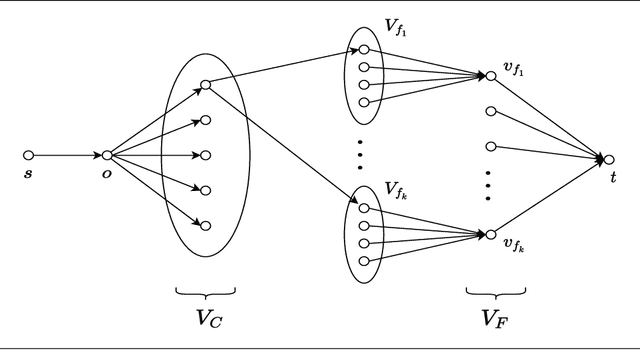
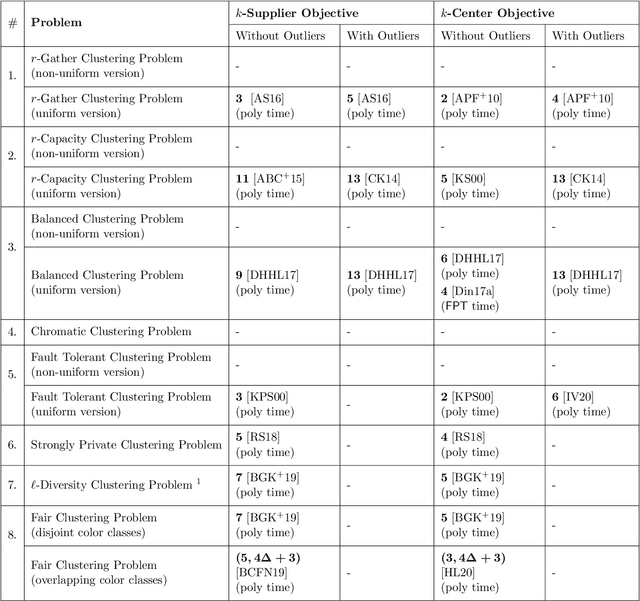
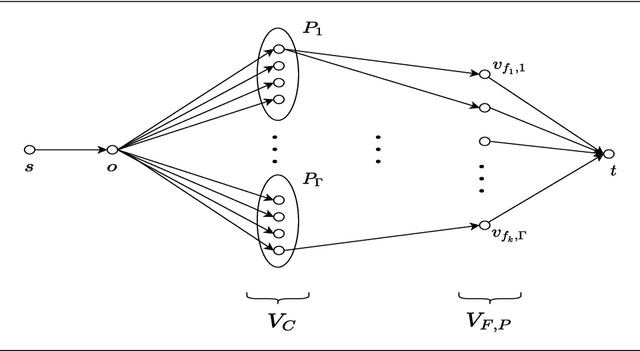
In this work, we study a range of constrained versions of the $k$-supplier and $k$-center problems such as: capacitated, fault-tolerant, fair, etc. These problems fall under a broad framework of constrained clustering. A unified framework for constrained clustering was proposed by Ding and Xu [SODA 2015] in context of the $k$-median and $k$-means objectives. In this work, we extend this framework to the $k$-supplier and $k$-center objectives. This unified framework allows us to obtain results simultaneously for the following constrained versions of the $k$-supplier problem: $r$-gather, $r$-capacity, balanced, chromatic, fault-tolerant, strongly private, $\ell$-diversity, and fair $k$-supplier problems, with and without outliers. We obtain the following results: We give $3$ and $2$ approximation algorithms for the constrained $k$-supplier and $k$-center problems, respectively, with $\mathsf{FPT}$ running time $k^{O(k)} \cdot n^{O(1)}$, where $n = |C \cup L|$. Moreover, these approximation guarantees are tight; that is, for any constant $\epsilon>0$, no algorithm can achieve $(3-\epsilon)$ and $(2-\epsilon)$ approximation guarantees for the constrained $k$-supplier and $k$-center problems in $\mathsf{FPT}$ time, assuming $\mathsf{FPT} \neq \mathsf{W}[2]$. Furthermore, we study these constrained problems in outlier setting. Our algorithm gives $3$ and $2$ approximation guarantees for the constrained outlier $k$-supplier and $k$-center problems, respectively, with $\mathsf{FPT}$ running time $(k+m)^{O(k)} \cdot n^{O(1)}$, where $n = |C \cup L|$ and $m$ is the number of outliers.

FPT Approximation for Socially Fair Clustering

In this work, we study the socially fair $k$-median/$k$-means problem. We are given a set of points $P$ in a metric space $\mathcal{X}$ with a distance function $d(.,.)$. There are $\ell$ groups: $P_1,\dotsc,P_{\ell} \subseteq P$. We are also given a set $F$ of feasible centers in $\mathcal{X}$. The goal of the socially fair $k$-median problem is to find a set $C \subseteq F$ of $k$ centers that minimizes the maximum average cost over all the groups. That is, find $C$ that minimizes the objective function $\Phi(C,P) \equiv \max_{j} \sum_{x \in P_j} d(C,x)/|P_j|$, where $d(C,x)$ is the distance of $x$ to the closest center in $C$. The socially fair $k$-means problem is defined similarly by using squared distances, i.e., $d^{2}(.,.)$ instead of $d(.,.)$. In this work, we design $(5+\varepsilon)$ and $(33 + \varepsilon)$ approximation algorithms for the socially fair $k$-median and $k$-means problems, respectively. For the parameters: $k$ and $\ell$, the algorithms have an FPT (fixed parameter tractable) running time of $f(k,\ell,\varepsilon) \cdot n$ for $f(k,\ell,\varepsilon) = 2^{{O}(k \, \ell/\varepsilon)}$ and $n = |P \cup F|$. We also study a special case of the problem where the centers are allowed to be chosen from the point set $P$, i.e., $P \subseteq F$. For this special case, our algorithms give better approximation guarantees of $(4+\varepsilon)$ and $(18+\varepsilon)$ for the socially fair $k$-median and $k$-means problems, respectively. Furthermore, we convert these algorithms to constant pass log-space streaming algorithms. Lastly, we show FPT hardness of approximation results for the problem with a small gap between our upper and lower bounds.

Hardness of Approximation of Euclidean $k$-Median

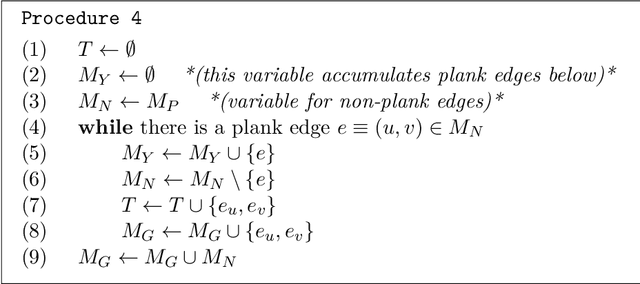
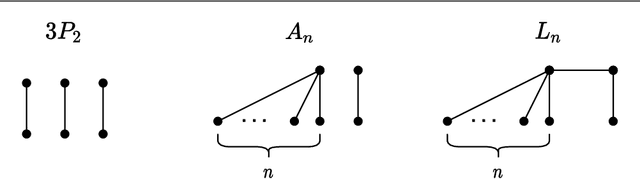
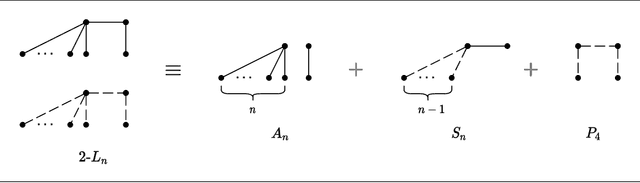
The Euclidean $k$-median problem is defined in the following manner: given a set $\mathcal{X}$ of $n$ points in $\mathbb{R}^{d}$, and an integer $k$, find a set $C \subset \mathbb{R}^{d}$ of $k$ points (called centers) such that the cost function $\Phi(C,\mathcal{X}) \equiv \sum_{x \in \mathcal{X}} \min_{c \in C} \|x-c\|_{2}$ is minimized. The Euclidean $k$-means problem is defined similarly by replacing the distance with squared distance in the cost function. Various hardness of approximation results are known for the Euclidean $k$-means problem. However, no hardness of approximation results were known for the Euclidean $k$-median problem. In this work, assuming the unique games conjecture (UGC), we provide the first hardness of approximation result for the Euclidean $k$-median problem. Furthermore, we study the hardness of approximation for the Euclidean $k$-means/$k$-median problems in the bi-criteria setting where an algorithm is allowed to choose more than $k$ centers. That is, bi-criteria approximation algorithms are allowed to output $\beta k$ centers (for constant $\beta>1$) and the approximation ratio is computed with respect to the optimal $k$-means/$k$-median cost. In this setting, we show the first hardness of approximation result for the Euclidean $k$-median problem for any $\beta < 1.015$, assuming UGC. We also show a similar bi-criteria hardness of approximation result for the Euclidean $k$-means problem with a stronger bound of $\beta < 1.28$, again assuming UGC.