Constraint programming model and biased random-key genetic algorithm for the single-machine coupled task scheduling problem with exact delays to minimize the makespan

We consider the strongly NP-hard single-machine coupled task scheduling problem with exact delays to minimize the makespan. In this problem, a set of jobs has to be scheduled, each composed of two tasks interspersed by an exact delay. Given that no preemption is allowed, the goal consists of minimizing the completion time of the last scheduled task. We model the problem using constraint programming (CP) and propose a biased random-key genetic algorithm (BRKGA). Our CP model applies well-established global constraints. Our BRKGA combines some successful components in the literature: an initial solution generator, periodical restarts and shakes, and a local search algorithm. Furthermore, the BRKGA's decoder is focused on efficiency rather than optimality, which accelerates the solution space exploration. Computational experiments on a benchmark set containing instances with up to 100 jobs (200 tasks) indicate that the proposed BRKGA can efficiently explore the problem solution space, providing high-quality approximate solutions within low computational times. It can also provide better solutions than the CP model under the same computational settings, i.e., three minutes of time limit and a single thread. The CP model, when offered a longer running time of 3600 seconds and multiple threads, significantly improved the results, reaching the current best-known solution for 90.56% of these instances. Finally, our experiments highlight the importance of the shake and local search components in the BRKGA, whose combination significantly improves the results of a standard BRKGA.

An enhanced simulation-based iterated local search metaheuristic for gravity fed water distribution network design optimization

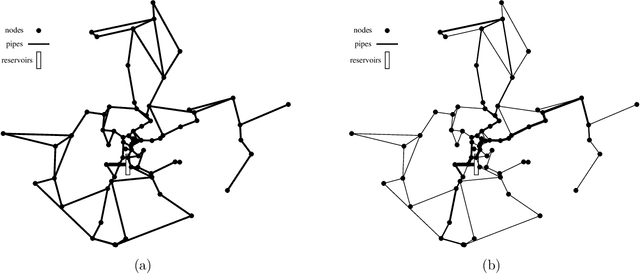
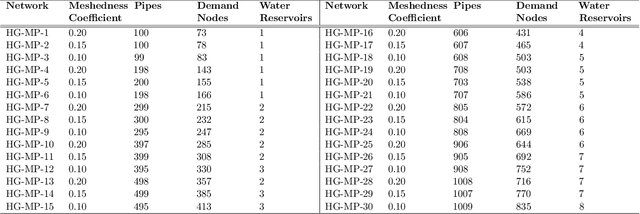
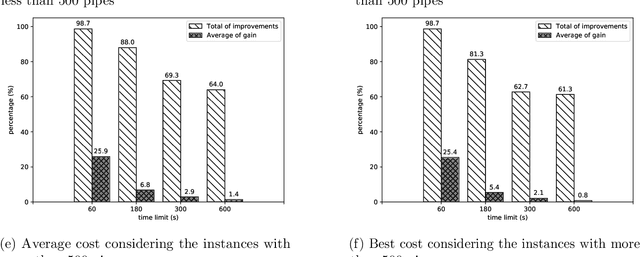
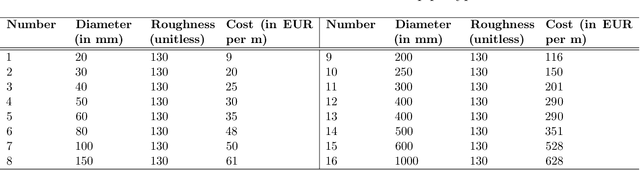
The gravity fed water distribution network design (WDND) optimization problem consists in determining the pipe diameters of a water network such that hydraulic constraints are satisfied and the total cost is minimized. Traditionally, such design decisions are made on the basis of expert experience. When networks increase in size, however, rules of thumb will rarely lead to near optimal decisions. Over the past thirty years, a large number of techniques have been developed to tackle the problem of optimally designing a water distribution network. In this paper, we tackle the NP-hard water distribution network design (WDND) optimization problem in a multi-period setting where time varying demand patterns occur. We propose a new simulation-based iterated local search metaheuristic which further explores the structure of the problem in an attempt to obtain high quality solutions. Computational experiments show that our approach is very competitive as it is able to improve over a state-of-the-art metaheuristic for most of the performed tests. Furthermore, it converges much faster to low cost solutions and demonstrates a more robust performance in that it obtains smaller deviations from the best known solutions.

A fast and effective MIP-based heuristic for a selective and periodic inventory routing problem in reverse logistics

We consider an NP-hard selective and periodic inventory routing problem (SPIRP) in a waste vegetable oil collection environment. This SPIRP arises in the context of reverse logistics where a biodiesel company has daily requirements of oil to be used as raw material in its production process. These requirements can be fulfilled by using the available inventory, collecting waste vegetable oil or purchasing virgin oil. The problem consists in determining a period (cyclic) planning for the collection and purchasing of oil such that the total collection, inventory and purchasing costs are minimized, while meeting the company's oil requirements and all the operational constraints. We propose a MIP-based heuristic which solves a relaxed model without routing, constructs routes taking into account the relaxation's solution and then improves these routes by solving the capacitated vehicle routing problem associated to each period. Following this approach, an a posteriori performance guarantee is ensured, as the approach provides both a lower bound and a feasible solution. The performed computational experiments show that the MIP-based heuristic is very fast and effective as it is able to encounter near optimal solutions with low gaps within seconds, improving several of the best known results using just a fraction of the time spent by a state-of-the-art heuristic. A remarkable fact is that the proposed MIP-based heuristic improves over the best known results for all the large instances available in the literature.