Discriminative Clustering with Relative Constraints

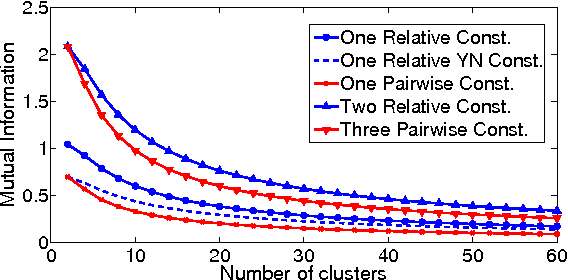
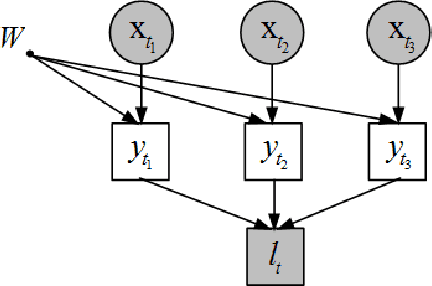
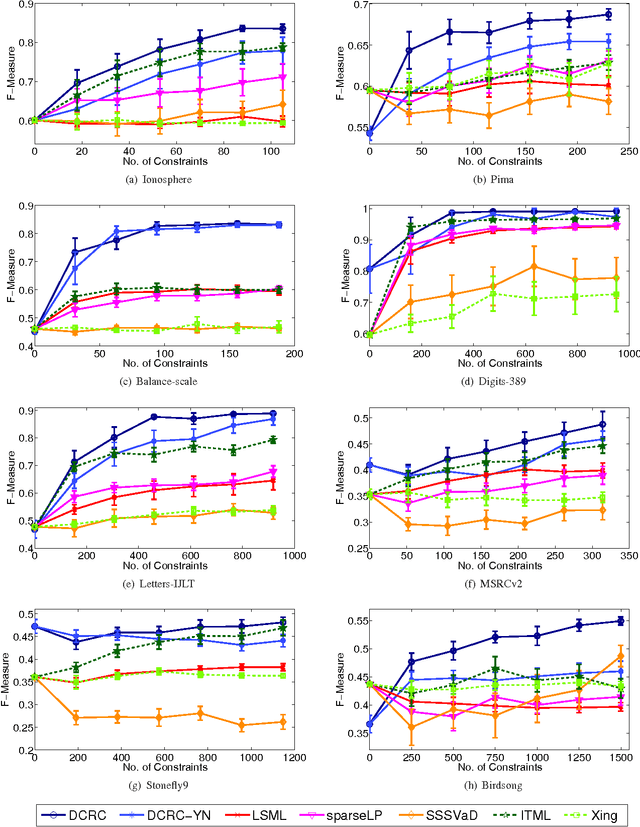
We study the problem of clustering with relative constraints, where each constraint specifies relative similarities among instances. In particular, each constraint $(x_i, x_j, x_k)$ is acquired by posing a query: is instance $x_i$ more similar to $x_j$ than to $x_k$? We consider the scenario where answers to such queries are based on an underlying (but unknown) class concept, which we aim to discover via clustering. Different from most existing methods that only consider constraints derived from yes and no answers, we also incorporate don't know responses. We introduce a Discriminative Clustering method with Relative Constraints (DCRC) which assumes a natural probabilistic relationship between instances, their underlying cluster memberships, and the observed constraints. The objective is to maximize the model likelihood given the constraints, and in the meantime enforce cluster separation and cluster balance by also making use of the unlabeled instances. We evaluated the proposed method using constraints generated from ground-truth class labels, and from (noisy) human judgments from a user study. Experimental results demonstrate: 1) the usefulness of relative constraints, in particular when don't know answers are considered; 2) the improved performance of the proposed method over state-of-the-art methods that utilize either relative or pairwise constraints; and 3) the robustness of our method in the presence of noisy constraints, such as those provided by human judgement.

Active Metric Learning from Relative Comparisons

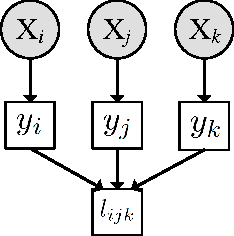
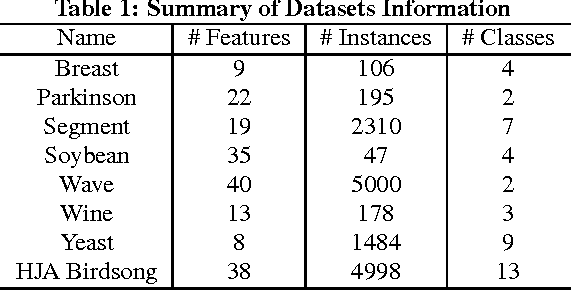
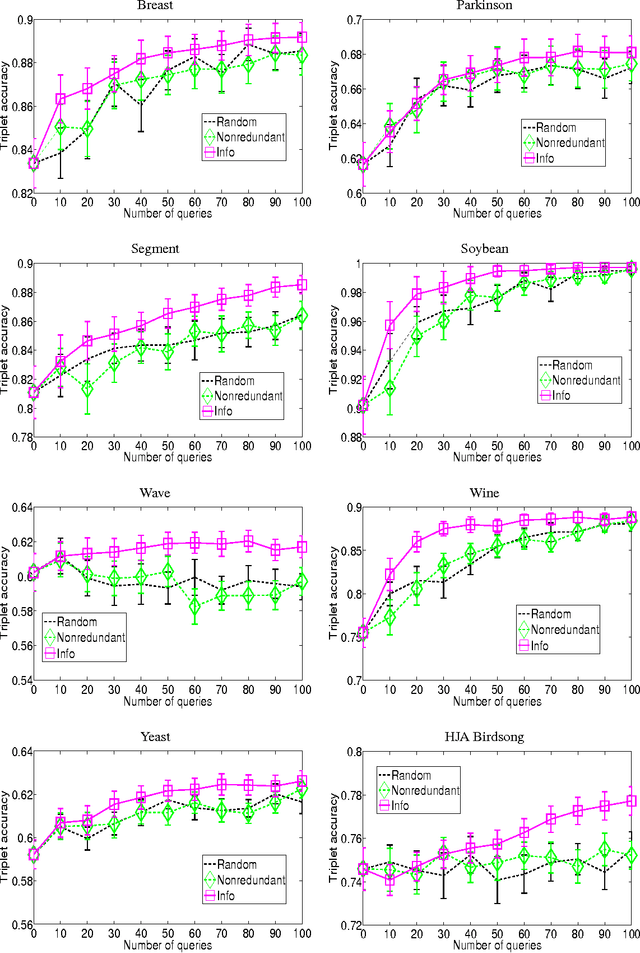
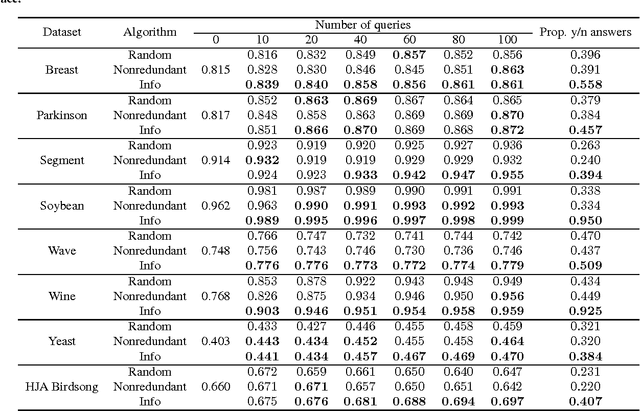
This work focuses on active learning of distance metrics from relative comparison information. A relative comparison specifies, for a data point triplet $(x_i,x_j,x_k)$, that instance $x_i$ is more similar to $x_j$ than to $x_k$. Such constraints, when available, have been shown to be useful toward defining appropriate distance metrics. In real-world applications, acquiring constraints often require considerable human effort. This motivates us to study how to select and query the most useful relative comparisons to achieve effective metric learning with minimum user effort. Given an underlying class concept that is employed by the user to provide such constraints, we present an information-theoretic criterion that selects the triplet whose answer leads to the highest expected gain in information about the classes of a set of examples. Directly applying the proposed criterion requires examining $O(n^3)$ triplets with $n$ instances, which is prohibitive even for datasets of moderate size. We show that a randomized selection strategy can be used to reduce the selection pool from $O(n^3)$ to $O(n)$, allowing us to scale up to larger-size problems. Experiments show that the proposed method consistently outperforms two baseline policies.