Tree-structured Ising models can be learned efficiently

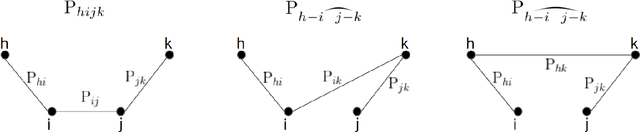
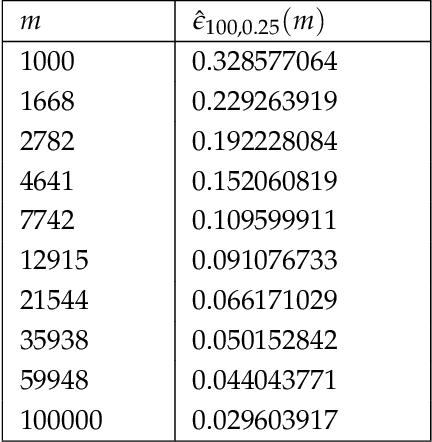
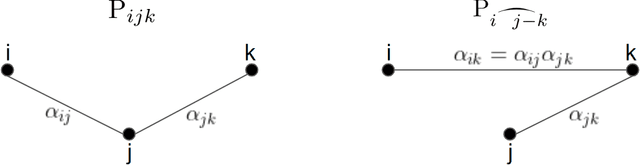
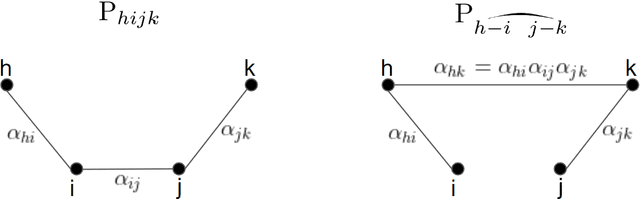
We provide the first polynomial-sample and polynomial-time algorithm for learning tree-structured Ising models. In particular, we show that $n$-variable tree-structured Ising models can be learned computationally-efficiently to within total variation distance~$\epsilon$ from an optimal $O(n \log n/\epsilon^2)$ samples, where $O(.)$ hides an absolute constant which does not depend on the model being learned -- neither its tree nor the magnitude of its edge strengths, on which we place no assumptions. Our guarantees hold, in fact, for the celebrated Chow-Liu [1968] algorithm, using the plug-in estimator for mutual information. While this (or any other) algorithm may fail to identify the structure of the underlying model correctly from a finite sample, we show that it will still learn a tree-structured model that is close to the true one in TV distance, a guarantee called "proper learning." Prior to our work there were no known sample- and time-efficient algorithms for learning (properly or non-properly) arbitrary tree-structured graphical models. In particular, our guarantees cannot be derived from known results for the Chow-Liu algorithm and the ensuing literature on learning graphical models, including a recent renaissance of algorithms on this learning challenge, which only yield asymptotic consistency results, or sample-inefficient and/or time-inefficient algorithms, unless further assumptions are placed on the graphical model, such as bounds on the "strengths" of the model's edges. While we establish guarantees for a widely known and simple algorithm, the analysis that this algorithm succeeds is quite complex, requiring a hierarchical classification of the edges into layers with different reconstruction guarantees, depending on their strength, combined with delicate uses of the subadditivity of the squared Hellinger distance over graphical models to control the error accumulation.

Square Hellinger Subadditivity for Bayesian Networks and its Applications to Identity Testing

We show that the square Hellinger distance between two Bayesian networks on the same directed graph, $G$, is subadditive with respect to the neighborhoods of $G$. Namely, if $P$ and $Q$ are the probability distributions defined by two Bayesian networks on the same DAG, our inequality states that the square Hellinger distance, $H^2(P,Q)$, between $P$ and $Q$ is upper bounded by the sum, $\sum_v H^2(P_{\{v\} \cup \Pi_v}, Q_{\{v\} \cup \Pi_v})$, of the square Hellinger distances between the marginals of $P$ and $Q$ on every node $v$ and its parents $\Pi_v$ in the DAG. Importantly, our bound does not involve the conditionals but the marginals of $P$ and $Q$. We derive a similar inequality for more general Markov Random Fields. As an application of our inequality, we show that distinguishing whether two Bayesian networks $P$ and $Q$ on the same (but potentially unknown) DAG satisfy $P=Q$ vs $d_{\rm TV}(P,Q)>\epsilon$ can be performed from $\tilde{O}(|\Sigma|^{3/4(d+1)} \cdot n/\epsilon^2)$ samples, where $d$ is the maximum in-degree of the DAG and $\Sigma$ the domain of each variable of the Bayesian networks. If $P$ and $Q$ are defined on potentially different and potentially unknown trees, the sample complexity becomes $\tilde{O}(|\Sigma|^{4.5} n/\epsilon^2)$, whose dependence on $n, \epsilon$ is optimal up to logarithmic factors. Lastly, if $P$ and $Q$ are product distributions over $\{0,1\}^n$ and $Q$ is known, the sample complexity becomes $O(\sqrt{n}/\epsilon^2)$, which is optimal up to constant factors.