Synthesis of timeline-based planning strategies avoiding determinization

Qualitative timeline-based planning models domains as sets of independent, but interacting, components whose behaviors over time, the timelines, are governed by sets of qualitative temporal constraints (ordering relations), called synchronization rules. Its plan-existence problem has been shown to be PSPACE-complete; in particular, PSPACE-membership has been proved via reduction to the nonemptiness problem for nondeterministic finite automata. However, nondeterministic automata cannot be directly used to synthesize planning strategies as a costly determinization step is needed. In this paper, we identify a fragment of qualitative timeline-based planning whose plan-existence problem can be directly mapped into the nonemptiness problem of deterministic finite automata, which can then synthesize strategies. In addition, we identify a maximal subset of Allen's relations that fits into such a deterministic fragment.

Begin, After, and Later: a Maximal Decidable Interval Temporal Logic

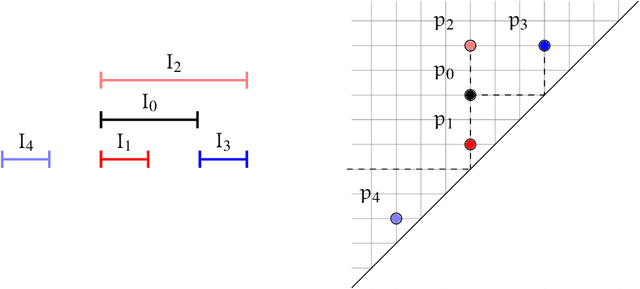
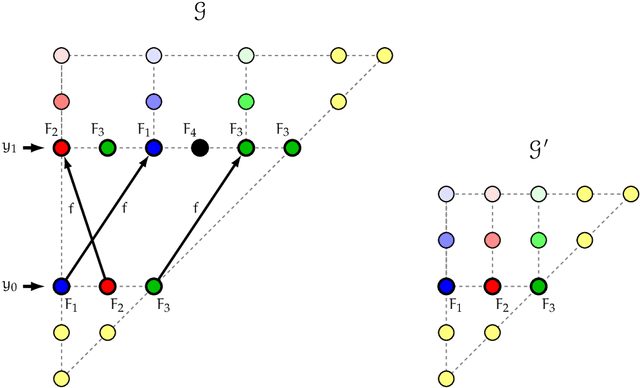
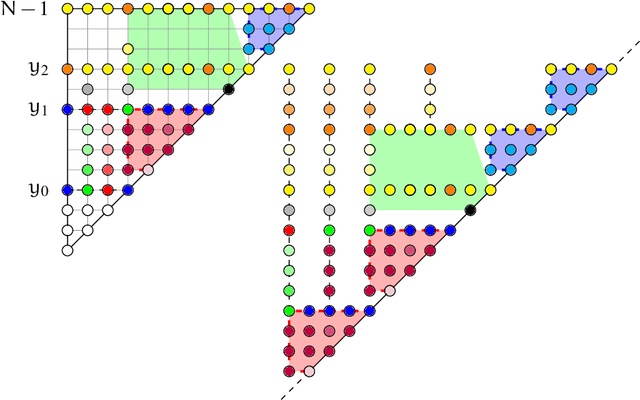
Interval temporal logics (ITLs) are logics for reasoning about temporal statements expressed over intervals, i.e., periods of time. The most famous ITL studied so far is Halpern and Shoham's HS, which is the logic of the thirteen Allen's interval relations. Unfortunately, HS and most of its fragments have an undecidable satisfiability problem. This discouraged the research in this area until recently, when a number non-trivial decidable ITLs have been discovered. This paper is a contribution towards the complete classification of all different fragments of HS. We consider different combinations of the interval relations Begins, After, Later and their inverses Abar, Bbar, and Lbar. We know from previous works that the combination ABBbarAbar is decidable only when finite domains are considered (and undecidable elsewhere), and that ABBbar is decidable over the natural numbers. We extend these results by showing that decidability of ABBar can be further extended to capture the language ABBbarLbar, which lays in between ABBar and ABBbarAbar, and that turns out to be maximal w.r.t decidability over strongly discrete linear orders (e.g. finite orders, the naturals, the integers). We also prove that the proposed decision procedure is optimal with respect to the complexity class.