Generalization Bounds of Surrogate Policies for Combinatorial Optimization Problems

A recent stream of structured learning approaches has improved the practical state of the art for a range of combinatorial optimization problems with complex objectives encountered in operations research. Such approaches train policies that chain a statistical model with a surrogate combinatorial optimization oracle to map any instance of the problem to a feasible solution. The key idea is to exploit the statistical distribution over instances instead of dealing with instances separately. However learning such policies by risk minimization is challenging because the empirical risk is piecewise constant in the parameters, and few theoretical guarantees have been provided so far. In this article, we investigate methods that smooth the risk by perturbing the policy, which eases optimization and improves generalization. Our main contribution is a generalization bound that controls the perturbation bias, the statistical learning error, and the optimization error. Our analysis relies on the introduction of a uniform weak property, which captures and quantifies the interplay of the statistical model and the surrogate combinatorial optimization oracle. This property holds under mild assumptions on the statistical model, the surrogate optimization, and the instance data distribution. We illustrate the result on a range of applications such as stochastic vehicle scheduling. In particular, such policies are relevant for contextual stochastic optimization and our results cover this case.

Mirror and Preconditioned Gradient Descent in Wasserstein Space

As the problem of minimizing functionals on the Wasserstein space encompasses many applications in machine learning, different optimization algorithms on $\mathbb{R}^d$ have received their counterpart analog on the Wasserstein space. We focus here on lifting two explicit algorithms: mirror descent and preconditioned gradient descent. These algorithms have been introduced to better capture the geometry of the function to minimize and are provably convergent under appropriate (namely relative) smoothness and convexity conditions. Adapting these notions to the Wasserstein space, we prove guarantees of convergence of some Wasserstein-gradient-based discrete-time schemes for new pairings of objective functionals and regularizers. The difficulty here is to carefully select along which curves the functionals should be smooth and convex. We illustrate the advantages of adapting the geometry induced by the regularizer on ill-conditioned optimization tasks, and showcase the improvement of choosing different discrepancies and geometries in a computational biology task of aligning single-cells.

Approximation of optimization problems with constraints through kernel Sum-Of-Squares

Handling an infinite number of inequality constraints in infinite-dimensional spaces occurs in many fields, from global optimization to optimal transport. These problems have been tackled individually in several previous articles through kernel Sum-Of-Squares (kSoS) approximations. We propose here a unified theorem to prove convergence guarantees for these schemes. Inequalities are turned into equalities to a class of nonnegative kSoS functions. This enables the use of scattering inequalities to mitigate the curse of dimensionality in sampling the constraints, leveraging the assumed smoothness of the functions appearing in the problem. This approach is illustrated in learning vector fields with side information, here the invariance of a set.

Mirror Descent with Relative Smoothness in Measure Spaces, with application to Sinkhorn and EM

Many problems in machine learning can be formulated as optimizing a convex functional over a space of measures. This paper studies the convergence of the mirror descent algorithm in this infinite-dimensional setting. Defining Bregman divergences through directional derivatives, we derive the convergence of the scheme for relatively smooth and strongly convex pairs of functionals. Applying our result to joint distributions and the Kullback--Leibler (KL) divergence, we show that Sinkhorn's primal iterations for entropic optimal transport in the continuous setting correspond to a mirror descent, and we obtain a new proof of its (sub)linear convergence. We also show that Expectation Maximization (EM) can always formally be written as a mirror descent, and, when optimizing on the latent distribution while fixing the mixtures, we derive sublinear rates of convergence.

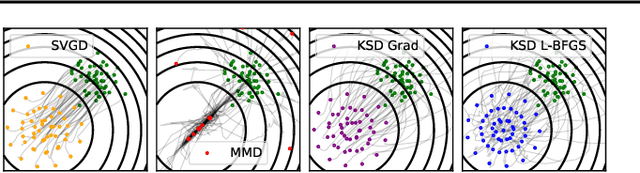
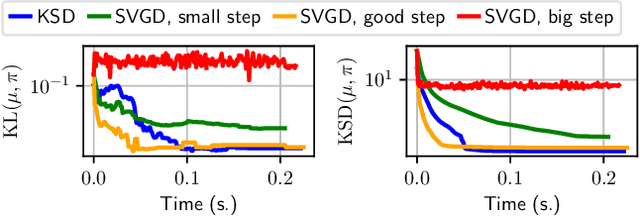
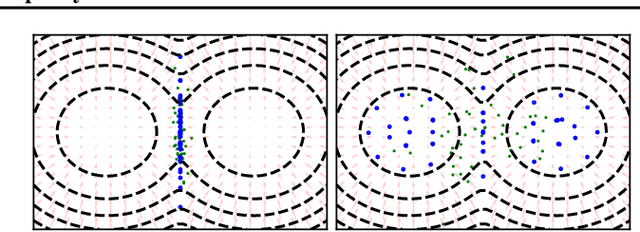
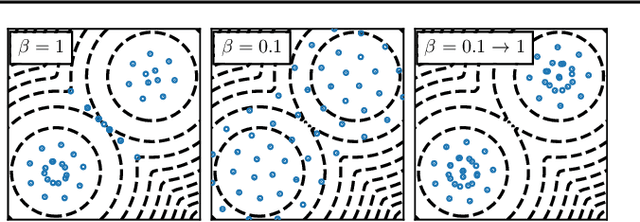
Kernel Stein Discrepancy Descent

Among dissimilarities between probability distributions, the Kernel Stein Discrepancy (KSD) has received much interest recently. We investigate the properties of its Wasserstein gradient flow to approximate a target probability distribution $\pi$ on $\mathbb{R}^d$, known up to a normalization constant. This leads to a straightforwardly implementable, deterministic score-based method to sample from $\pi$, named KSD Descent, which uses a set of particles to approximate $\pi$. Remarkably, owing to a tractable loss function, KSD Descent can leverage robust parameter-free optimization schemes such as L-BFGS; this contrasts with other popular particle-based schemes such as the Stein Variational Gradient Descent algorithm. We study the convergence properties of KSD Descent and demonstrate its practical relevance. However, we also highlight failure cases by showing that the algorithm can get stuck in spurious local minima.

Handling Hard Affine SDP Shape Constraints in RKHSs

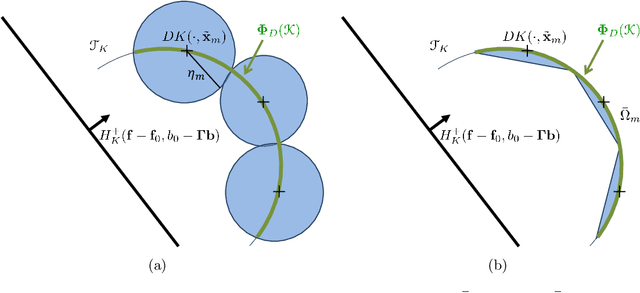
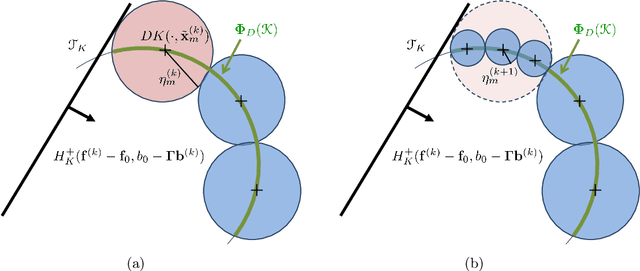
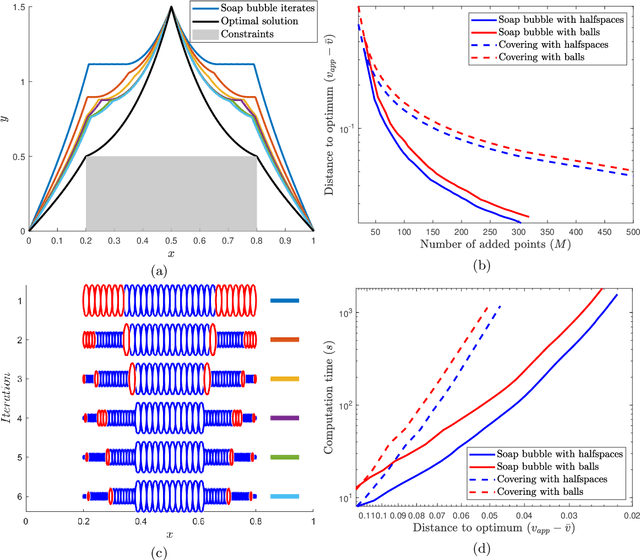
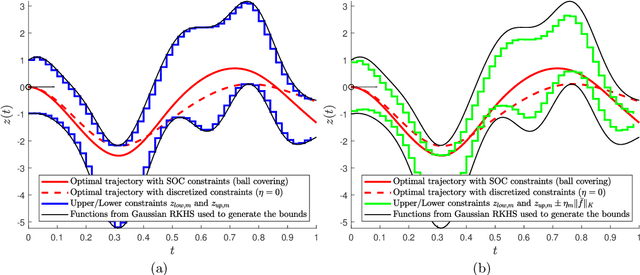
Shape constraints, such as non-negativity, monotonicity, convexity or supermodularity, play a key role in various applications of machine learning and statistics. However, incorporating this side information into predictive models in a hard way (for example at all points of an interval) for rich function classes is a notoriously challenging problem. We propose a unified and modular convex optimization framework, relying on second-order cone (SOC) tightening, to encode hard affine SDP constraints on function derivatives, for models belonging to vector-valued reproducing kernel Hilbert spaces (vRKHSs). The modular nature of the proposed approach allows to simultaneously handle multiple shape constraints, and to tighten an infinite number of constraints into finitely many. We prove the consistency of the proposed scheme and that of its adaptive variant, leveraging geometric properties of vRKHSs. The efficiency of the approach is illustrated in the context of shape optimization, safety-critical control and econometrics.

Hard Shape-Constrained Kernel Machines

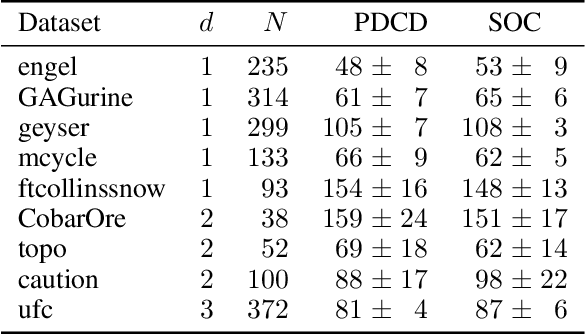
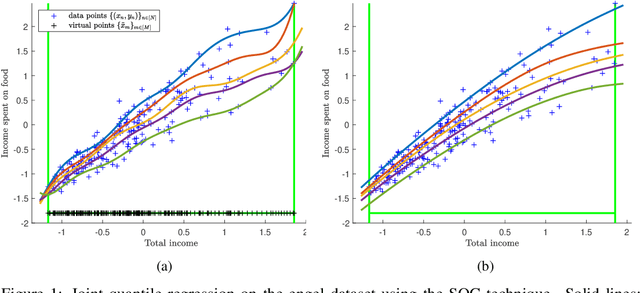
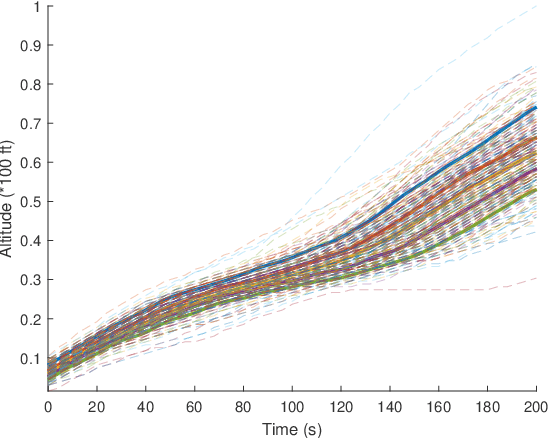
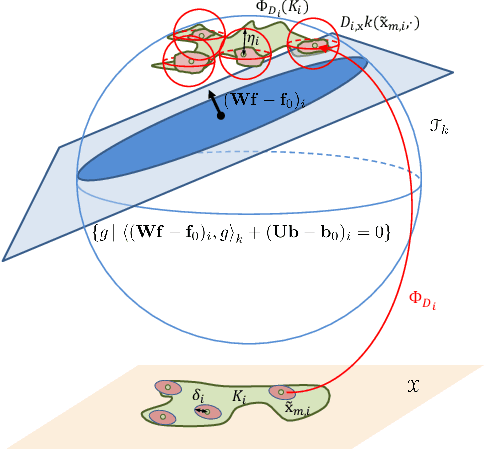
Shape constraints (such as non-negativity, monotonicity, convexity) play a central role in a large number of applications, as they usually improve performance for small sample size and help interpretability. However enforcing these shape requirements in a hard fashion is an extremely challenging problem. Classically, this task is tackled (i) in a soft way (without out-of-sample guarantees), (ii) by specialized transformation of the variables on a case-by-case basis, or (iii) by using highly restricted function classes, such as polynomials or polynomial splines. In this paper, we prove that hard affine shape constraints on function derivatives can be encoded in kernel machines which represent one of the most flexible and powerful tools in machine learning and statistics. Particularly, we present a tightened second-order cone constrained reformulation, that can be readily implemented in convex solvers. We prove performance guarantees on the solution, and demonstrate the efficiency of the approach in joint quantile regression with applications to economics and to the analysis of aircraft trajectories, among others.