Pierre C Bellec
Simultaneous analysis of approximate leave-one-out cross-validation and mean-field inference
Jan 05, 2025Abstract:Approximate Leave-One-Out Cross-Validation (ALO-CV) is a method that has been proposed to estimate the generalization error of a regularized estimator in the high-dimensional regime where dimension and sample size are of the same order, the so called ``proportional regime''. A new analysis is developed to derive the consistency of ALO-CV for non-differentiable regularizer under Gaussian covariates and strong-convexity of the regularizer. Using a conditioning argument, the difference between the ALO-CV weights and their counterparts in mean-field inference is shown to be small. Combined with upper bounds between the mean-field inference estimate and the leave-one-out quantity, this provides a proof that ALO-CV approximates the leave-one-out quantity as well up to negligible error terms. Linear models with square loss, robust linear regression and single-index models are explicitly treated.
Noise Covariance Estimation in Multi-Task High-dimensional Linear Models
Jun 15, 2022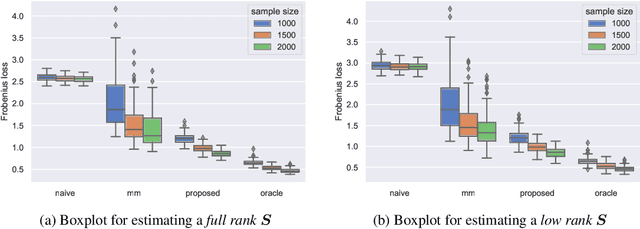
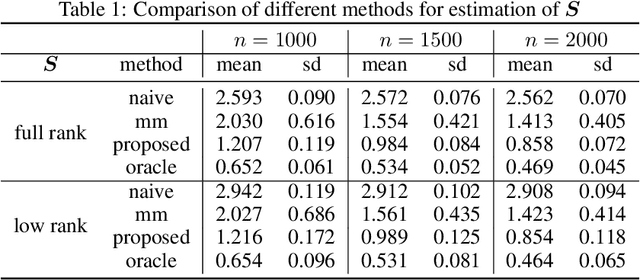
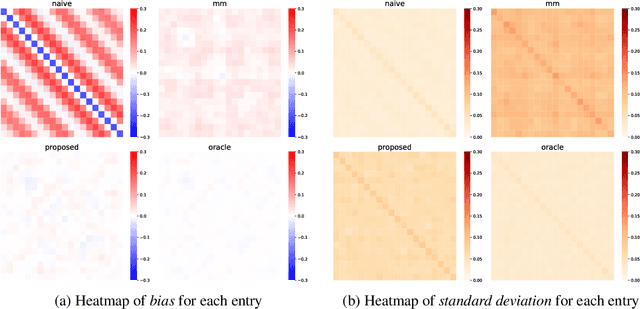
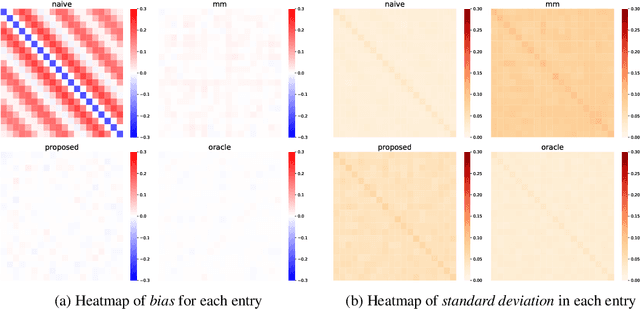
Abstract:This paper studies the multi-task high-dimensional linear regression models where the noise among different tasks is correlated, in the moderately high dimensional regime where sample size $n$ and dimension $p$ are of the same order. Our goal is to estimate the covariance matrix of the noise random vectors, or equivalently the correlation of the noise variables on any pair of two tasks. Treating the regression coefficients as a nuisance parameter, we leverage the multi-task elastic-net and multi-task lasso estimators to estimate the nuisance. By precisely understanding the bias of the squared residual matrix and by correcting this bias, we develop a novel estimator of the noise covariance that converges in Frobenius norm at the rate $n^{-1/2}$ when the covariates are Gaussian. This novel estimator is efficiently computable. Under suitable conditions, the proposed estimator of the noise covariance attains the same rate of convergence as the "oracle" estimator that knows in advance the regression coefficients of the multi-task model. The Frobenius error bounds obtained in this paper also illustrate the advantage of this new estimator compared to a method-of-moments estimator that does not attempt to estimate the nuisance. As a byproduct of our techniques, we obtain an estimate of the generalization error of the multi-task elastic-net and multi-task lasso estimators. Extensive simulation studies are carried out to illustrate the numerical performance of the proposed method.
Observable adjustments in single-index models for regularized M-estimators
Apr 14, 2022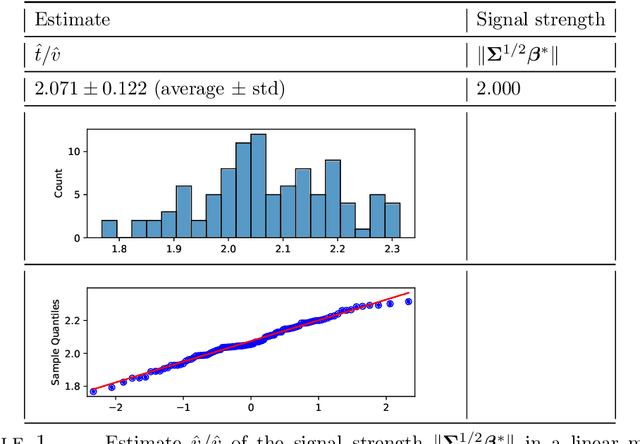

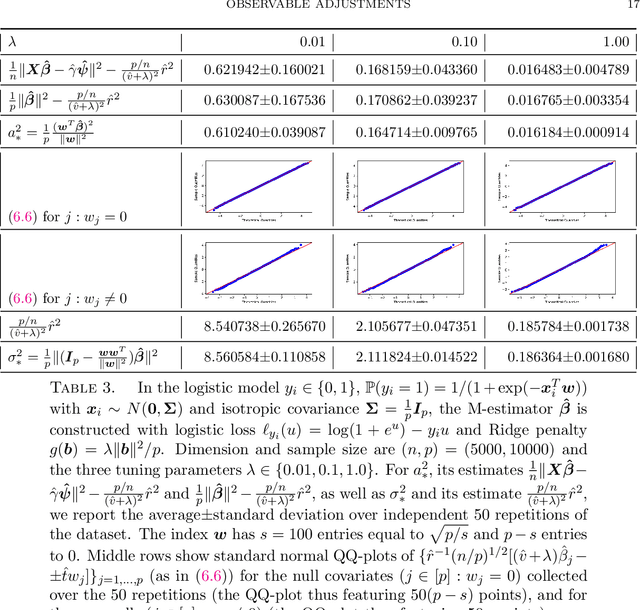
Abstract:We consider observations $(X,y)$ from single index models with unknown link function, Gaussian covariates and a regularized M-estimator $\hat\beta$ constructed from convex loss function and regularizer. In the regime where sample size $n$ and dimension $p$ are both increasing such that $p/n$ has a finite limit, the behavior of the empirical distribution of $\hat\beta$ and the predicted values $X\hat\beta$ has been previously characterized in a number of models: The empirical distributions are known to converge to proximal operators of the loss and penalty in a related Gaussian sequence model, which captures the interplay between ratio $p/n$, loss, regularization and the data generating process. This connection between$(\hat\beta,X\hat\beta)$ and the corresponding proximal operators require solving fixed-point equations that typically involve unobservable quantities such as the prior distribution on the index or the link function. This paper develops a different theory to describe the empirical distribution of $\hat\beta$ and $X\hat\beta$: Approximations of $(\hat\beta,X\hat\beta)$ in terms of proximal operators are provided that only involve observable adjustments. These proposed observable adjustments are data-driven, e.g., do not require prior knowledge of the index or the link function. These new adjustments yield confidence intervals for individual components of the index, as well as estimators of the correlation of $\hat\beta$ with the index. The interplay between loss, regularization and the model is thus captured in a data-driven manner, without solving the fixed-point equations studied in previous works. The results apply to both strongly convex regularizers and unregularized M-estimation. Simulations are provided for the square and logistic loss in single index models including logistic regression and 1-bit compressed sensing with 20\% corrupted bits.
Chi-square and normal inference in high-dimensional multi-task regression
Jul 16, 2021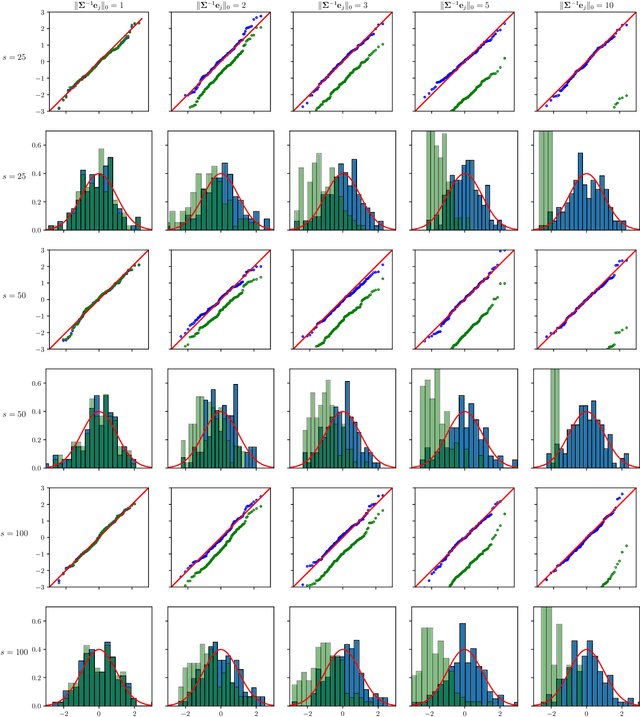
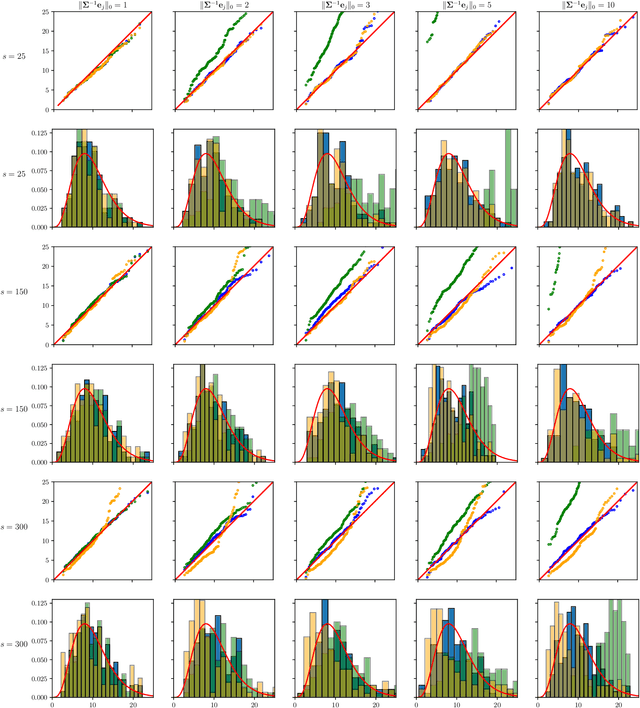
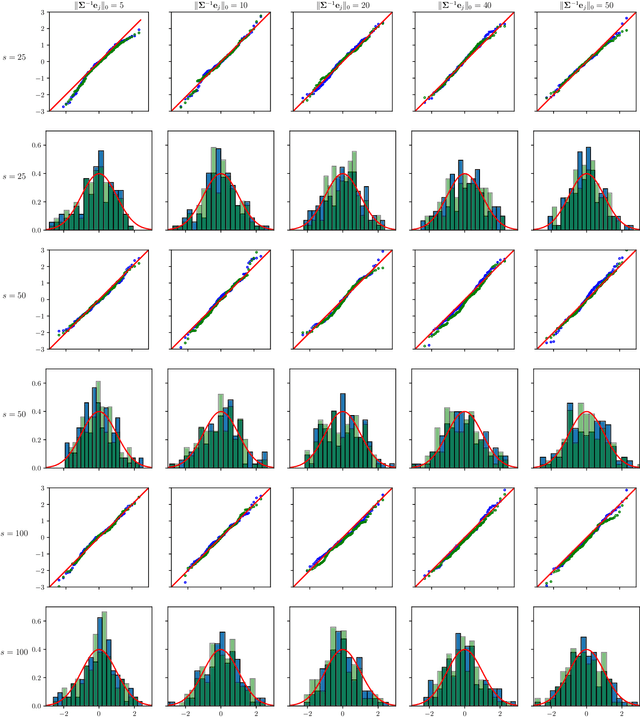
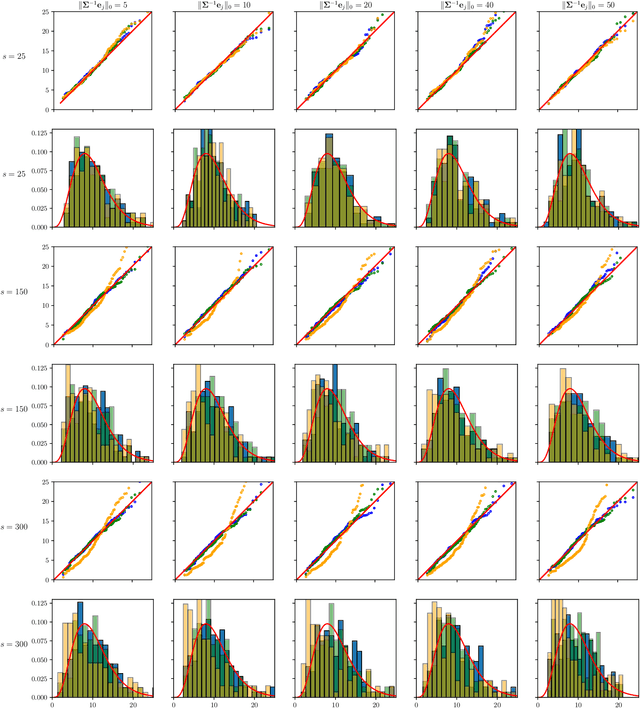
Abstract:The paper proposes chi-square and normal inference methodologies for the unknown coefficient matrix $B^*$ of size $p\times T$ in a Multi-Task (MT) linear model with $p$ covariates, $T$ tasks and $n$ observations under a row-sparse assumption on $B^*$. The row-sparsity $s$, dimension $p$ and number of tasks $T$ are allowed to grow with $n$. In the high-dimensional regime $p\ggg n$, in order to leverage row-sparsity, the MT Lasso is considered. We build upon the MT Lasso with a de-biasing scheme to correct for the bias induced by the penalty. This scheme requires the introduction of a new data-driven object, coined the interaction matrix, that captures effective correlations between noise vector and residuals on different tasks. This matrix is psd, of size $T\times T$ and can be computed efficiently. The interaction matrix lets us derive asymptotic normal and $\chi^2_T$ results under Gaussian design and $\frac{sT+s\log(p/s)}{n}\to0$ which corresponds to consistency in Frobenius norm. These asymptotic distribution results yield valid confidence intervals for single entries of $B^*$ and valid confidence ellipsoids for single rows of $B^*$, for both known and unknown design covariance $\Sigma$. While previous proposals in grouped-variables regression require row-sparsity $s\lesssim\sqrt n$ up to constants depending on $T$ and logarithmic factors in $n,p$, the de-biasing scheme using the interaction matrix provides confidence intervals and $\chi^2_T$ confidence ellipsoids under the conditions ${\min(T^2,\log^8p)}/{n}\to 0$ and $$ \frac{sT+s\log(p/s)+\|\Sigma^{-1}e_j\|_0\log p}{n}\to0, \quad \frac{\min(s,\|\Sigma^{-1}e_j\|_0)}{\sqrt n} \sqrt{[T+\log(p/s)]\log p}\to 0, $$ allowing row-sparsity $s\ggg\sqrt n$ when $\|\Sigma^{-1}e_j\|_0 \sqrt T\lll \sqrt{n}$ up to logarithmic factors.
Derivatives and residual distribution of regularized M-estimators with application to adaptive tuning
Jul 11, 2021
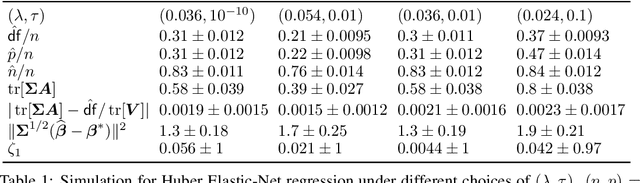

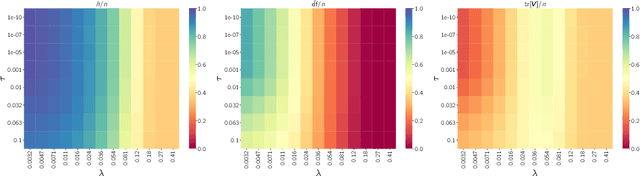
Abstract:This paper studies M-estimators with gradient-Lipschitz loss function regularized with convex penalty in linear models with Gaussian design matrix and arbitrary noise distribution. A practical example is the robust M-estimator constructed with the Huber loss and the Elastic-Net penalty and the noise distribution has heavy-tails. Our main contributions are three-fold. (i) We provide general formulae for the derivatives of regularized M-estimators $\hat\beta(y,X)$ where differentiation is taken with respect to both $y$ and $X$; this reveals a simple differentiability structure shared by all convex regularized M-estimators. (ii) Using these derivatives, we characterize the distribution of the residual $r_i = y_i-x_i^\top\hat\beta$ in the intermediate high-dimensional regime where dimension and sample size are of the same order. (iii) Motivated by the distribution of the residuals, we propose a novel adaptive criterion to select tuning parameters of regularized M-estimators. The criterion approximates the out-of-sample error up to an additive constant independent of the estimator, so that minimizing the criterion provides a proxy for minimizing the out-of-sample error. The proposed adaptive criterion does not require the knowledge of the noise distribution or of the covariance of the design. Simulated data confirms the theoretical findings, regarding both the distribution of the residuals and the success of the criterion as a proxy of the out-of-sample error. Finally our results reveal new relationships between the derivatives of $\hat\beta(y,X)$ and the effective degrees of freedom of the M-estimator, which are of independent interest.
Asymptotic normality of robust $M$-estimators with convex penalty
Jul 08, 2021
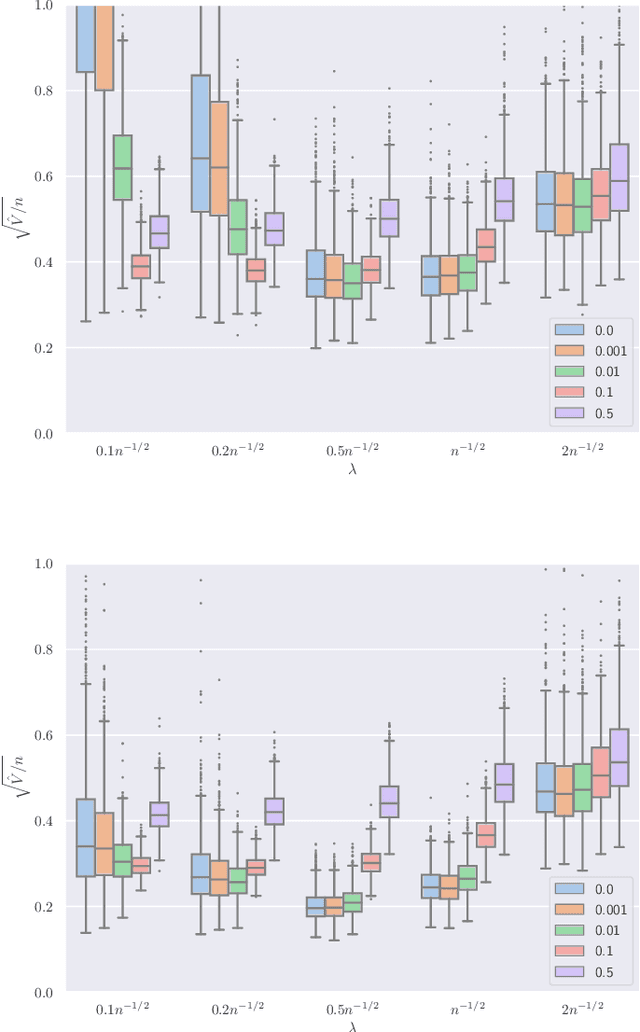

Abstract:This paper develops asymptotic normality results for individual coordinates of robust M-estimators with convex penalty in high-dimensions, where the dimension $p$ is at most of the same order as the sample size $n$, i.e, $p/n\le\gamma$ for some fixed constant $\gamma>0$. The asymptotic normality requires a bias correction and holds for most coordinates of the M-estimator for a large class of loss functions including the Huber loss and its smoothed versions regularized with a strongly convex penalty. The asymptotic variance that characterizes the width of the resulting confidence intervals is estimated with data-driven quantities. This estimate of the variance adapts automatically to low ($p/n\to0)$ or high ($p/n \le \gamma$) dimensions and does not involve the proximal operators seen in previous works on asymptotic normality of M-estimators. For the Huber loss, the estimated variance has a simple expression involving an effective degrees-of-freedom as well as an effective sample size. The case of the Huber loss with Elastic-Net penalty is studied in details and a simulation study confirms the theoretical findings. The asymptotic normality results follow from Stein formulae for high-dimensional random vectors on the sphere developed in the paper which are of independent interest.
Out-of-sample error estimate for robust M-estimators with convex penalty
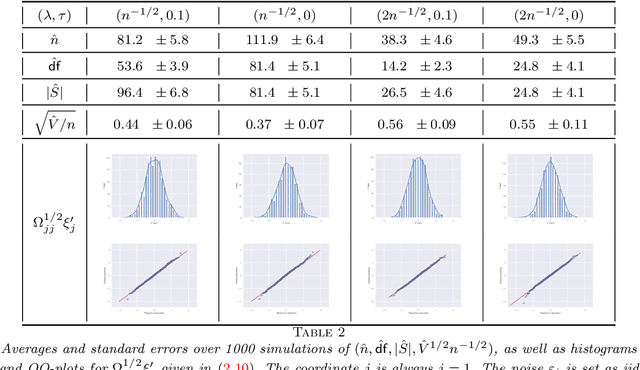
Sep 14, 2020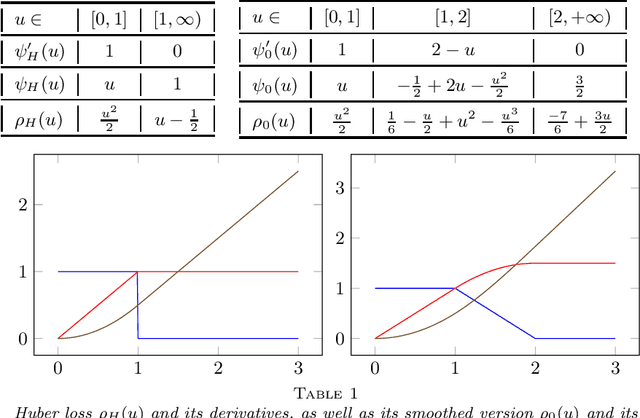

Abstract:A generic out-of-sample error estimate is proposed for robust $M$-estimators regularized with a convex penalty in high-dimensional linear regression where $(X,y)$ is observed and $p,n$ are of the same order. If $\psi$ is the derivative of the robust data-fitting loss $\rho$, the estimate depends on the observed data only through the quantities $\hat\psi = \psi(y-X\hat\beta)$, $X^\top \hat\psi$ and the derivatives $(\partial/\partial y) \hat\psi$ and $(\partial/\partial y) X\hat\beta$ for fixed $X$. The out-of-sample error estimate enjoys a relative error of order $n^{-1/2}$ in a linear model with Gaussian covariates and independent noise, either non-asymptotically when $p/n\le \gamma$ or asymptotically in the high-dimensional asymptotic regime $p/n\to\gamma'\in(0,\infty)$. General differentiable loss functions $\rho$ are allowed provided that $\psi=\rho'$ is 1-Lipschitz. The validity of the out-of-sample error estimate holds either under a strong convexity assumption, or for the $\ell_1$-penalized Huber M-estimator if the number of corrupted observations and sparsity of the true $\beta$ are bounded from above by $s_*n$ for some small enough constant $s_*\in(0,1)$ independent of $n,p$. For the square loss and in the absence of corruption in the response, the results additionally yield $n^{-1/2}$-consistent estimates of the noise variance and of the generalization error. This generalizes, to arbitrary convex penalty, estimates that were previously known for the Lasso.
First order expansion of convex regularized estimators
Oct 12, 2019Abstract:We consider first order expansions of convex penalized estimators in high-dimensional regression problems with random designs. Our setting includes linear regression and logistic regression as special cases. For a given penalty function $h$ and the corresponding penalized estimator $\hat\beta$, we construct a quantity $\eta$, the first order expansion of $\hat\beta$, such that the distance between $\hat\beta$ and $\eta$ is an order of magnitude smaller than the estimation error $\|\hat{\beta} - \beta^*\|$. In this sense, the first order expansion $\eta$ can be thought of as a generalization of influence functions from the mathematical statistics literature to regularized estimators in high-dimensions. Such first order expansion implies that the risk of $\hat{\beta}$ is asymptotically the same as the risk of $\eta$ which leads to a precise characterization of the MSE of $\hat\beta$; this characterization takes a particularly simple form for isotropic design. Such first order expansion also leads to inference results based on $\hat{\beta}$. We provide sufficient conditions for the existence of such first order expansion for three regularizers: the Lasso in its constrained form, the lasso in its penalized form, and the Group-Lasso. The results apply to general loss functions under some conditions and those conditions are satisfied for the squared loss in linear regression and for the logistic loss in the logistic model.
The cost-free nature of optimally tuning Tikhonov regularizers and other ordered smoothers
May 29, 2019Abstract:We consider the problem of selecting the best estimator among a family of Tikhonov regularized estimators, or, alternatively, to select a linear combination of these regularizers that is as good as the best regularizer in the family. Our theory reveals that if the Tikhonov regularizers share the same penalty matrix with different tuning parameters, a convex procedure based on $Q$-aggregation achieves the mean square error of the best estimator, up to a small error term no larger than $C\sigma^2$, where $\sigma^2$ is the noise level and $C>0$ is an absolute constant. Remarkably, the error term does not depend on the penalty matrix or the number of estimators as long as they share the same penalty matrix, i.e., it applies to any grid of tuning parameters, no matter how large the cardinality of the grid is. This reveals the surprising "cost-free" nature of optimally tuning Tikhonov regularizers, in striking contrast with the existing literature on aggregation of estimators where one typically has to pay a cost of $\sigma^2\log(M)$ where $M$ is the number of estimators in the family. The result holds, more generally, for any family of ordered linear smoothers. This encompasses Ridge regression as well as Principal Component Regression. The result is extended to the problem of tuning Tikhonov regularizers with different penalty matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge