Demystifying active inference

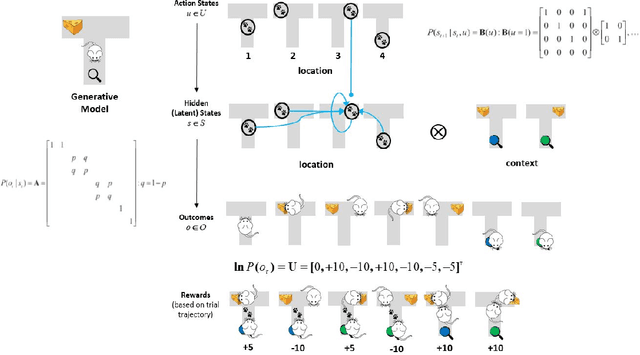
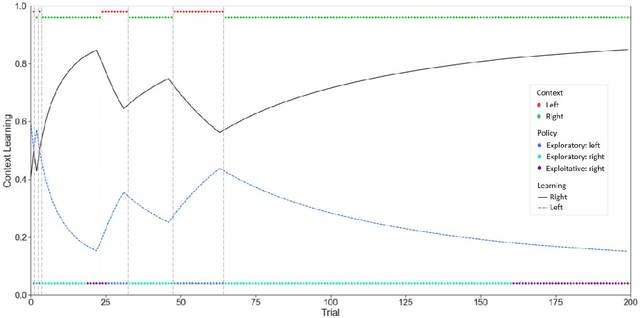
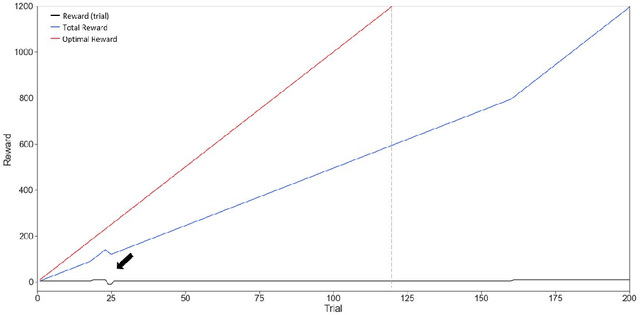
Active inference is a first (Bayesian) principles account of how autonomous agents might operate in dynamic, non-stationary environments. The optimization of congruent formulations of the free energy functional (variational and expected), in active inference, enables agents to make inferences about the environment and select optimal behaviors. The agent achieves this by evaluating (sensory) evidence in relation to its internal generative model that entails beliefs about future (hidden) states and sequence of actions that it can choose. In contrast to analogous frameworks $-$ by operating in a pure belief-based setting (free energy functional of beliefs about states) $-$ active inference agents can carry out epistemic exploration and naturally account for uncertainty about their environment. Through this review, we disambiguate these properties, by providing a condensed overview of the theory underpinning active inference. A T-maze simulation is used to demonstrate how these behaviors emerge naturally, as the agent makes inferences about the observed outcomes and optimizes its generative model (via belief updating). Additionally, the discrete state-space and time formulation presented provides an accessible guide on how to derive the (variational and expected) free energy equations and belief updating rules. We conclude by noting that this formalism can be applied in other engineering applications; e.g., robotic arm movement, playing Atari games, etc., if appropriate underlying probability distributions (i.e. generative model) can be formulated.

The Sensitivity of Counterfactual Fairness to Unmeasured Confounding

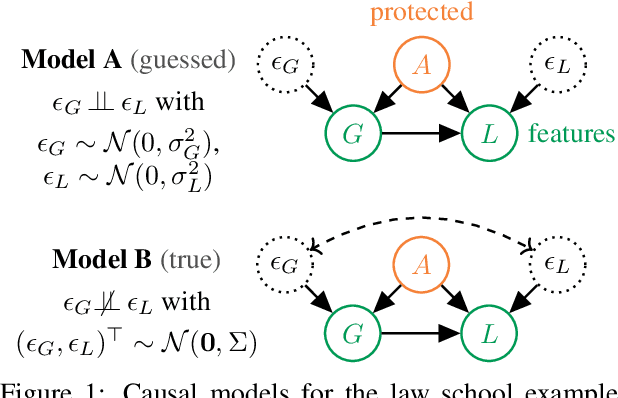
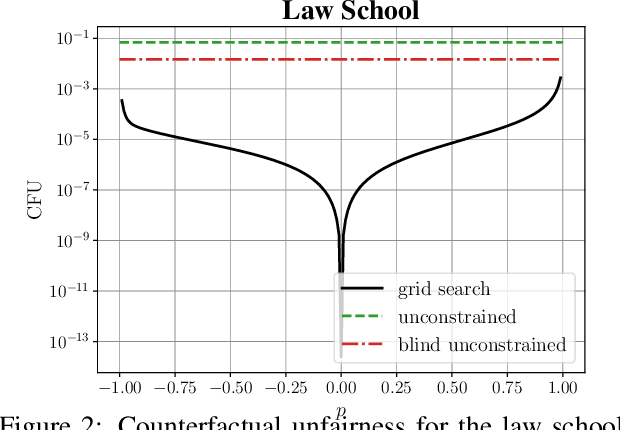
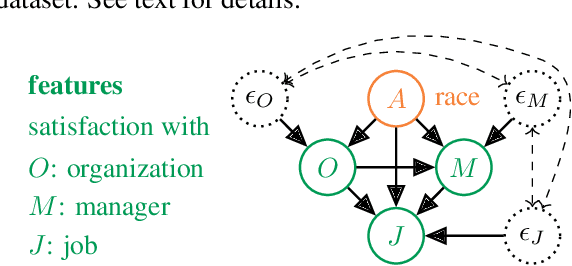
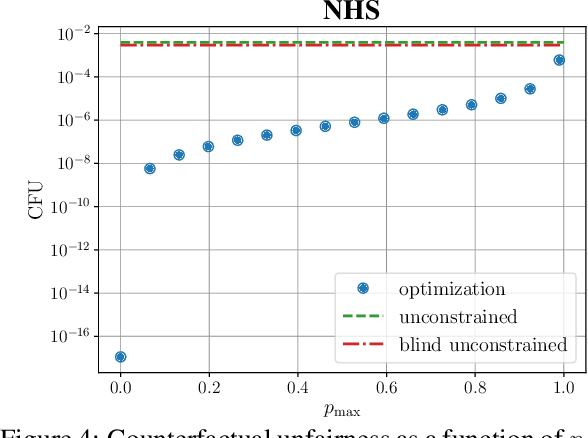
Causal approaches to fairness have seen substantial recent interest, both from the machine learning community and from wider parties interested in ethical prediction algorithms. In no small part, this has been due to the fact that causal models allow one to simultaneously leverage data and expert knowledge to remove discriminatory effects from predictions. However, one of the primary assumptions in causal modeling is that you know the causal graph. This introduces a new opportunity for bias, caused by misspecifying the causal model. One common way for misspecification to occur is via unmeasured confounding: the true causal effect between variables is partially described by unobserved quantities. In this work we design tools to assess the sensitivity of fairness measures to this confounding for the popular class of non-linear additive noise models (ANMs). Specifically, we give a procedure for computing the maximum difference between two counterfactually fair predictors, where one has become biased due to confounding. For the case of bivariate confounding our technique can be swiftly computed via a sequence of closed-form updates. For multivariate confounding we give an algorithm that can be efficiently solved via automatic differentiation. We demonstrate our new sensitivity analysis tools in real-world fairness scenarios to assess the bias arising from confounding.