Equivariant Filter for Relative Attitude and Target Angular Velocity Estimation

Accurate estimation of the relative attitude and angular velocity between two rigid bodies is fundamental in aerospace applications such as spacecraft rendezvous and docking. In these scenarios, a chaser vehicle must determine the orientation and angular velocity of a target object using onboard sensors. This work addresses the challenge of designing an Equivariant Filter (EqF) that can reliably estimate both the relative attitude and the target angular velocity using noisy observations of two known, non-collinear vectors fixed in the target frame. To derive the EqF, a symmetry for the system is proposed and an equivariant lift onto the symmetry group is calculated. Observability and convergence properties are analyzed. Simulations demonstrate the filter's performance, with Monte Carlo runs yielding statistically significant results. The impact of low-rate measurements is also examined and a strategy to mitigate this effect is proposed. Experimental results, using fiducial markers and both conventional and event cameras for measurement acquisition, further validate the approach, confirming its effectiveness in a realistic setting.

Convex MPC and Thrust Allocation with Deadband for Spacecraft Rendezvous

This paper delves into a rendezvous scenario involving a chaser and a target spacecraft, focusing on the application of Model Predictive Control (MPC) to design a controller capable of guiding the chaser toward the target. The operational principle of spacecraft thrusters, requiring a minimum activation time that leads to the existence of a control deadband, introduces mixed-integer constraints into the optimization, posing a considerable computational challenge due to the exponential complexity on the number of integer constraints. We address this complexity by presenting two solver algorithms that efficiently approximate the optimal solution in significantly less time than standard solvers, making them well-suited for real-time applications.

COSMIC: fast closed-form identification from large-scale data for LTV systems

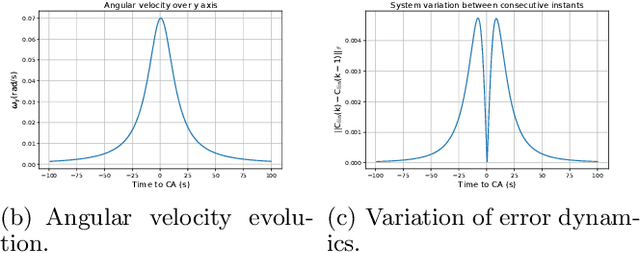
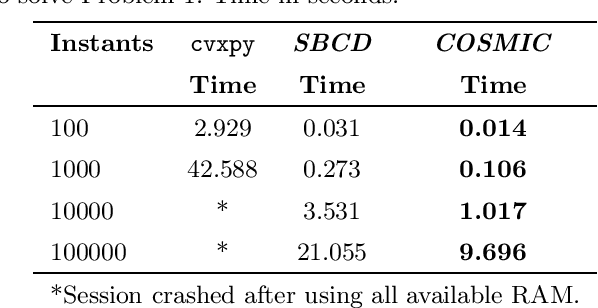
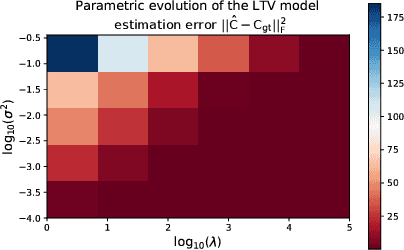
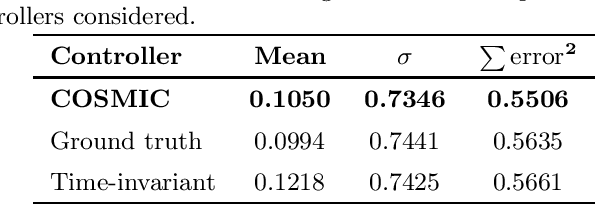
We introduce a closed-form method for identification of discrete-time linear time-variant systems from data, formulating the learning problem as a regularized least squares problem where the regularizer favors smooth solutions within a trajectory. We develop a closed-form algorithm with guarantees of optimality and with a complexity that increases linearly with the number of instants considered per trajectory. The COSMIC algorithm achieves the desired result even in the presence of large volumes of data. Our method solved the problem using two orders of magnitude less computational power than a general purpose convex solver and was about 3 times faster than a Stochastic Block Coordinate Descent especially designed method. Computational times of our method remained in the order of magnitude of the second even for 10k and 100k time instants, where the general purpose solver crashed. To prove its applicability to real world systems, we test with spring-mass-damper system and use the estimated model to find the optimal control path. Our algorithm was applied to both a Low Fidelity and Functional Engineering Simulators for the Comet Interceptor mission, that requires precise pointing of the on-board cameras in a fast dynamics environment. Thus, this paper provides a fast alternative to classical system identification techniques for linear time-variant systems, while proving to be a solid base for applications in the Space industry and a step forward to the incorporation of algorithms that leverage data in such a safety-critical environment.