Clustering Molecular Energy Landscapes by Adaptive Network Embedding

In order to efficiently explore the chemical space of all possible small molecules, a common approach is to compress the dimension of the system to facilitate downstream machine learning tasks. Towards this end, we present a data driven approach for clustering potential energy landscapes of molecular structures by applying recently developed Network Embedding techniques, to obtain latent variables defined through the embedding function. To scale up the method, we also incorporate an entropy sensitive adaptive scheme for hierarchical sampling of the energy landscape, based on Metadynamics and Transition Path Theory. By taking into account the kinetic information implied by a system's energy landscape, we are able to interpret dynamical node-node relationships in reduced dimensions. We demonstrate the framework through Lennard-Jones (LJ) clusters and a human DNA sequence.

Network Embedding Using Sparse Approximations of Random Walks

In this paper, we propose an efficient numerical implementation of Network Embedding based on commute times, using sparse approximation of a diffusion process on the network obtained by a modified version of the diffusion wavelet algorithm. The node embeddings are computed by optimizing the cross entropy loss via the stochastic gradient descent method with sampling of low-dimensional representations of green functions. We demonstrate the efficacy of this method for data clustering and multi-label classification through several examples, and compare its performance over existing methods in terms of efficiency and accuracy. Theoretical issues justifying the scheme are also discussed.

Identifying Transition States of Chemical Kinetic Systems using Network Embedding Techniques

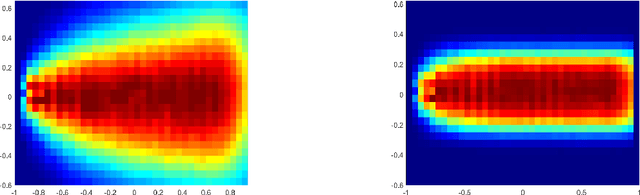
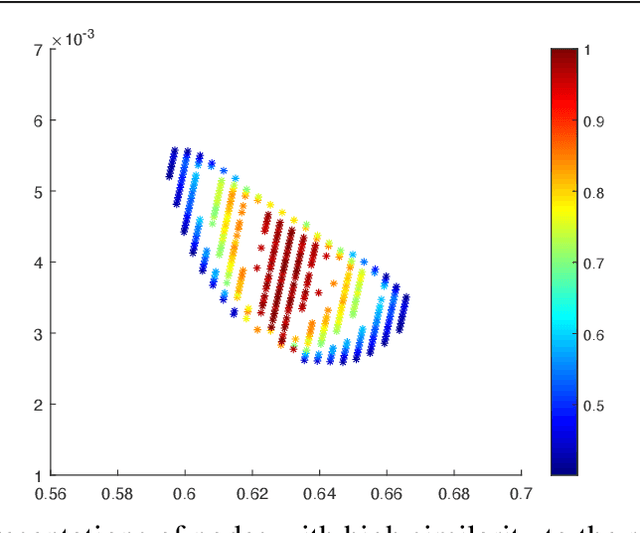
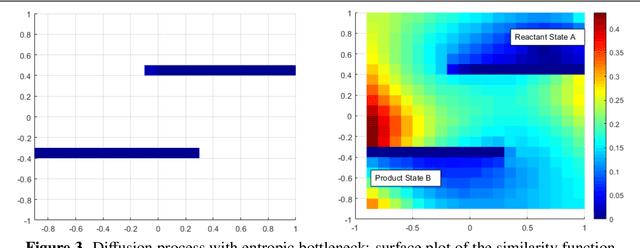
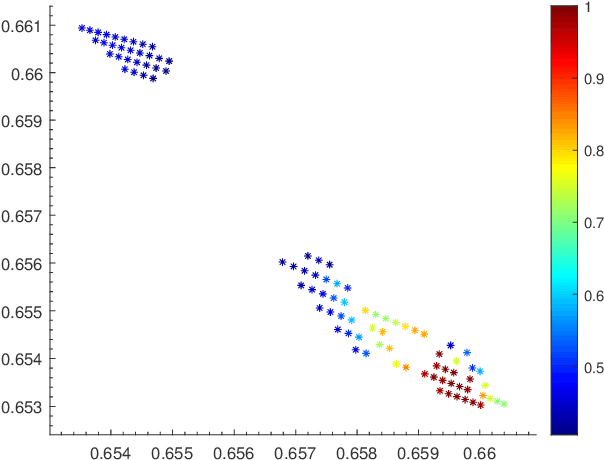
Using random walk sampling methods for feature learning on networks, we develop a method for generating low-dimensional node embeddings for directed graphs and identifying transition states of stochastic chemical reacting systems. We modified objective functions adopted in existing random walk based network embedding methods to handle directed graphs and neighbors of different degrees. Through optimization via gradient ascent, we embed the weighted graph vertices into a low-dimensional vector space Rd while preserving the neighborhood of each node. We then demonstrate the effectiveness of the method on dimension reduction through several examples regarding identification of transition states of chemical reactions, especially for entropic systems.