A Unified Theory of Compositionality, Modularity, and Interpretability in Markov Decision Processes

We introduce Option Kernel Bellman Equations (OKBEs) for a new reward-free Markov Decision Process. Rather than a value function, OKBEs directly construct and optimize a predictive map called a state-time option kernel (STOK) to maximize the probability of completing a goal while avoiding constraint violations. STOKs are compositional, modular, and interpretable initiation-to-termination transition kernels for policies in the Options Framework of Reinforcement Learning. This means: 1) STOKs can be composed using Chapman-Kolmogorov equations to make spatiotemporal predictions for multiple policies over long horizons, 2) high-dimensional STOKs can be represented and computed efficiently in a factorized and reconfigurable form, and 3) STOKs record the probabilities of semantically interpretable goal-success and constraint-violation events, needed for formal verification. Given a high-dimensional state-transition model for an intractable planning problem, we can decompose it with local STOKs and goal-conditioned policies that are aggregated into a factorized goal kernel, making it possible to forward-plan at the level of goals in high-dimensions to solve the problem. These properties lead to highly flexible agents that can rapidly synthesize meta-policies, reuse planning representations across many tasks, and justify goals using empowerment, an intrinsic motivation function. We argue that reward-maximization is in conflict with the properties of compositionality, modularity, and interpretability. Alternatively, OKBEs facilitate these properties to support verifiable long-horizon planning and intrinsic motivation that scales to dynamic high-dimensional world-models.

Constraint Satisfaction Propagation: Non-stationary Policy Synthesis for Temporal Logic Planning

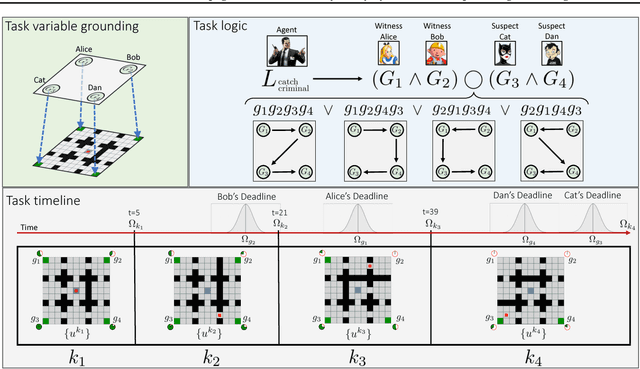
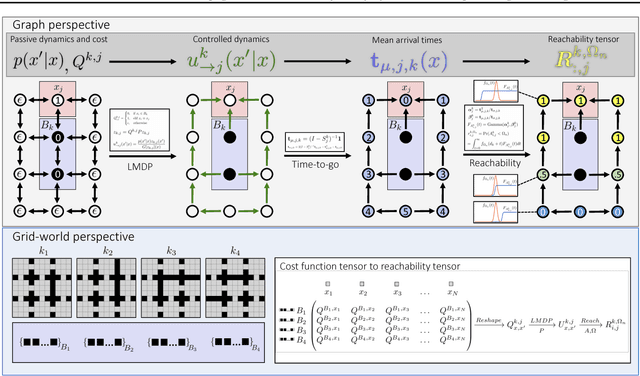
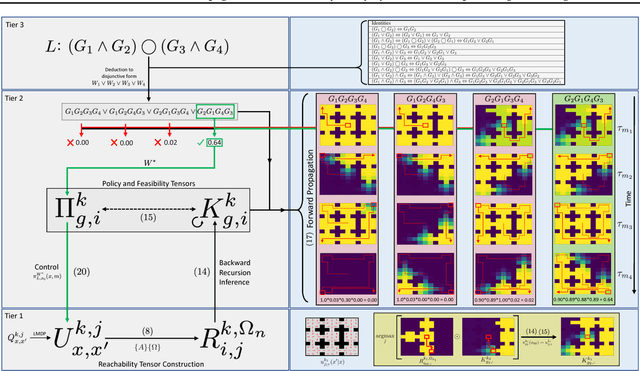
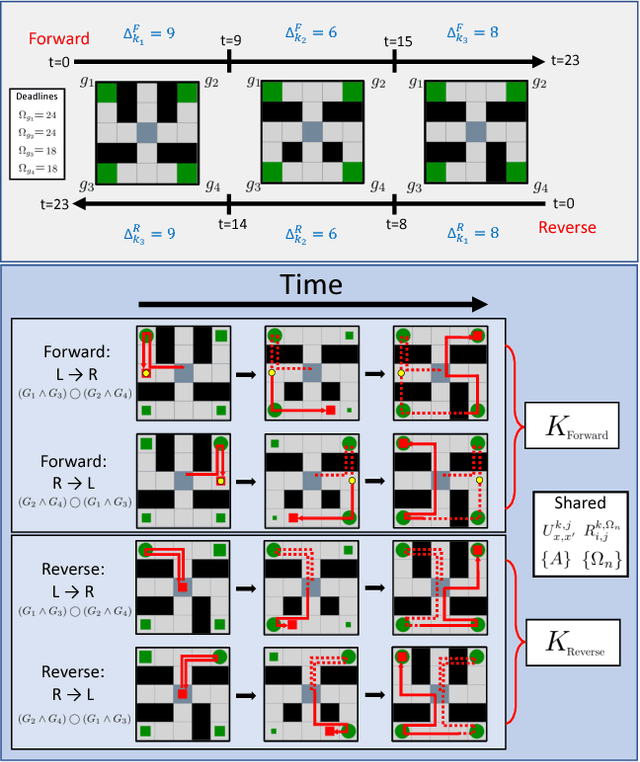
Problems arise when using reward functions to capture dependencies between sequential time-constrained goal states because the state-space must be prohibitively expanded to accommodate a history of successfully achieved sub-goals. Policies and value functions derived with stationarity assumptions are not readily decomposable, leading to a tension between reward maximization and task generalization. We demonstrate a logic-compatible approach using model-based knowledge of environment dynamics and deadline information to directly infer non-stationary policies composed of reusable stationary policies. The policies are constructed to maximize the probability of satisfying time-sensitive goals while respecting time-varying obstacles. Our approach explicitly maintains two different spaces, a high-level logical task specification where the task-variables are grounded onto the low-level state-space of a Markov decision process. Computing satisfiability at the task-level is made possible by a Bellman-like equation which operates on a tensor that links the temporal relationship between the two spaces; the equation solves for a value function that can be explicitly interpreted as the probability of sub-goal satisfaction under the synthesized non-stationary policy, an approach we term Constraint Satisfaction Propagation (CSP).