Assessing Look-Ahead Bias in Stock Return Predictions Generated By GPT Sentiment Analysis

Large language models (LLMs), including ChatGPT, can extract profitable trading signals from the sentiment in news text. However, backtesting such strategies poses a challenge because LLMs are trained on many years of data, and backtesting produces biased results if the training and backtesting periods overlap. This bias can take two forms: a look-ahead bias, in which the LLM may have specific knowledge of the stock returns that followed a news article, and a distraction effect, in which general knowledge of the companies named interferes with the measurement of a text's sentiment. We investigate these sources of bias through trading strategies driven by the sentiment of financial news headlines. We compare trading performance based on the original headlines with de-biased strategies in which we remove the relevant company's identifiers from the text. In-sample (within the LLM training window), we find, surprisingly, that the anonymized headlines outperform, indicating that the distraction effect has a greater impact than look-ahead bias. This tendency is particularly strong for larger companies--companies about which we expect an LLM to have greater general knowledge. Out-of-sample, look-ahead bias is not a concern but distraction remains possible. Our proposed anonymization procedure is therefore potentially useful in out-of-sample implementation, as well as for de-biased backtesting.

Should Bank Stress Tests Be Fair?

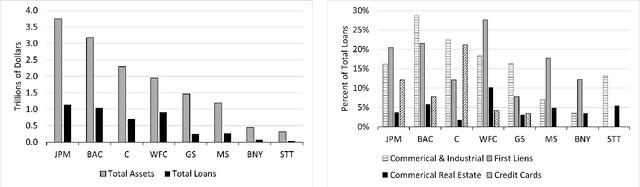
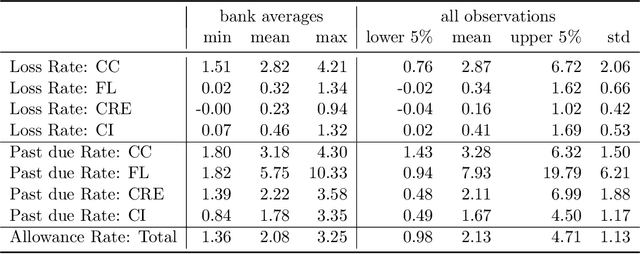
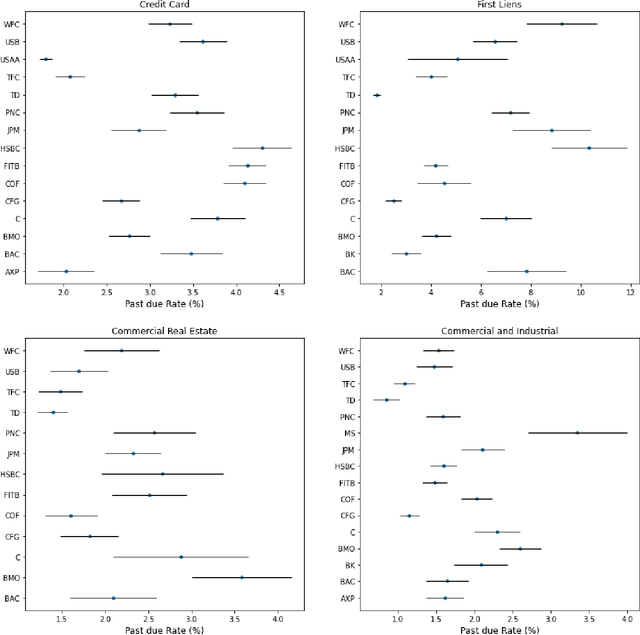
Regulatory stress tests have become the primary tool for setting capital requirements at the largest U.S. banks. The Federal Reserve uses confidential models to evaluate bank-specific outcomes for bank-specific portfolios in shared stress scenarios. As a matter of policy, the same models are used for all banks, despite considerable heterogeneity across institutions; individual banks have contended that some models are not suited to their businesses. Motivated by this debate, we ask, what is a fair aggregation of individually tailored models into a common model? We argue that simply pooling data across banks treats banks equally but is subject to two deficiencies: it may distort the impact of legitimate portfolio features, and it is vulnerable to implicit misdirection of legitimate information to infer bank identity. We compare various notions of regression fairness to address these deficiencies, considering both forecast accuracy and equal treatment. In the setting of linear models, we argue for estimating and then discarding centered bank fixed effects as preferable to simply ignoring differences across banks. We present evidence that the overall impact can be material. We also discuss extensions to nonlinear models.

Linear Classifiers Under Infinite Imbalance

We study the behavior of linear discriminant functions for binary classification in the infinite-imbalance limit, where the sample size of one class grows without bound while the sample size of the other remains fixed. The coefficients of the classifier minimize an expected loss specified through a weight function. We show that for a broad class of weight functions, the intercept diverges but the rest of the coefficient vector has a finite limit under infinite imbalance, extending prior work on logistic regression. The limit depends on the left tail of the weight function, for which we distinguish three cases: bounded, asymptotically polynomial, and asymptotically exponential. The limiting coefficient vectors reflect robustness or conservatism properties in the sense that they optimize against certain worst-case alternatives. In the bounded and polynomial cases, the limit is equivalent to an implicit choice of upsampling distribution for the minority class. We apply these ideas in a credit risk setting, with particular emphasis on performance in the high-sensitivity and high-specificity regions.

Choosing News Topics to Explain Stock Market Returns

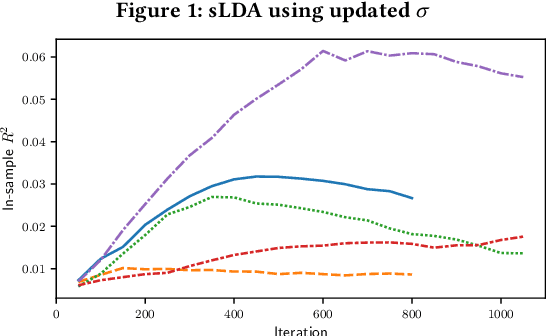
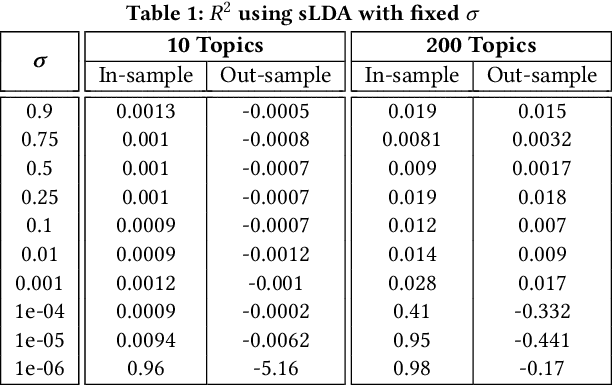
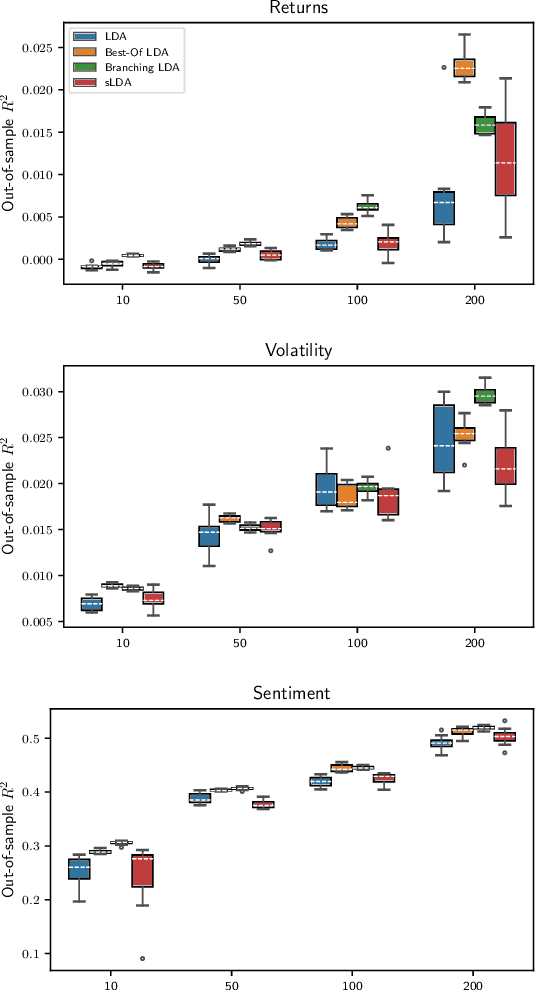
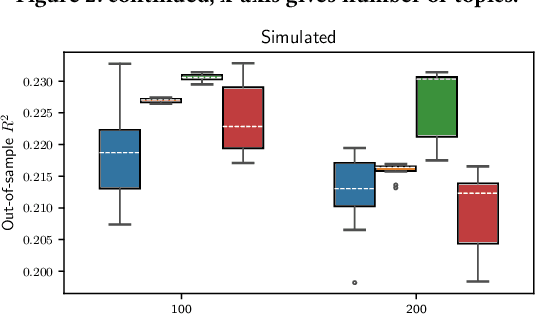
We analyze methods for selecting topics in news articles to explain stock returns. We find, through empirical and theoretical results, that supervised Latent Dirichlet Allocation (sLDA) implemented through Gibbs sampling in a stochastic EM algorithm will often overfit returns to the detriment of the topic model. We obtain better out-of-sample performance through a random search of plain LDA models. A branching procedure that reinforces effective topic assignments often performs best. We test methods on an archive of over 90,000 news articles about S&P 500 firms.