Entropic optimal transport beyond product reference couplings: the Gaussian case on Euclidean space

The optimal transport problem with squared Euclidean cost consists in finding a coupling between two input measures that maximizes correlation. Consequently, the optimal coupling is often singular with respect to Lebesgue measure. Regularizing the optimal transport problem with an entropy term yields an approximation called entropic optimal transport. Entropic penalties steer the induced coupling toward a reference measure with desired properties. For instance, when seeking a diffuse coupling, the most popular reference measures are the Lebesgue measure and the product of the two input measures. In this work, we study the case where the reference coupling is not necessarily assumed to be a product. We focus on the Gaussian case as a motivating paradigm, and provide a reduction of this more general optimal transport criterion to a matrix optimization problem. This reduction enables us to provide a complete description of the solution, both in terms of the primal variable and the dual variables. We argue that flexibility in terms of the reference measure can be important in statistical contexts, for instance when one has prior information, when there is uncertainty regarding the measures to be coupled, or to reduce bias when the entropic problem is used to estimate the un-regularized transport problem. In particular, we show in numerical examples that choosing a suitable reference plan allows to reduce the bias caused by the entropic penalty.

On the potential benefits of entropic regularization for smoothing Wasserstein estimators

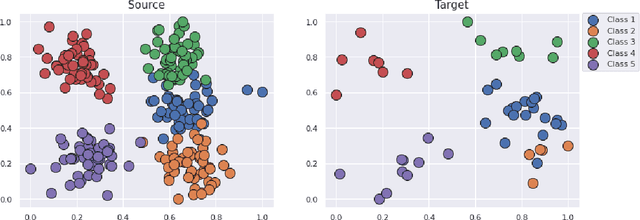
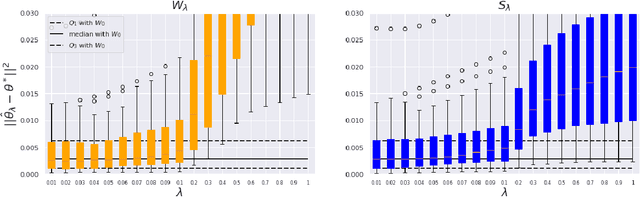
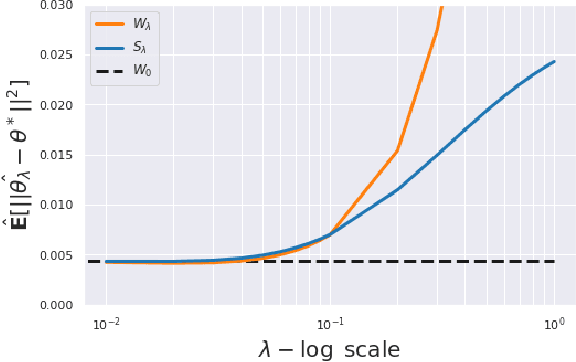
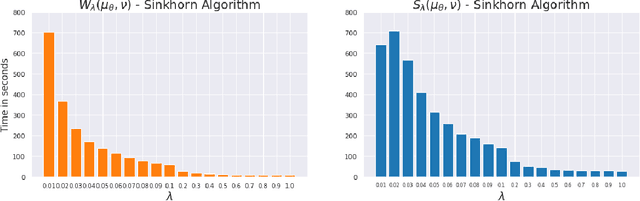
This paper is focused on the study of entropic regularization in optimal transport as a smoothing method for Wasserstein estimators, through the prism of the classical tradeoff between approximation and estimation errors in statistics. Wasserstein estimators are defined as solutions of variational problems whose objective function involves the use of an optimal transport cost between probability measures. Such estimators can be regularized by replacing the optimal transport cost by its regularized version using an entropy penalty on the transport plan. The use of such a regularization has a potentially significant smoothing effect on the resulting estimators. In this work, we investigate its potential benefits on the approximation and estimation properties of regularized Wasserstein estimators. Our main contribution is to discuss how entropic regularization may reach, at a lowest computational cost, statistical performances that are comparable to those of un-regularized Wasserstein estimators in statistical learning problems involving distributional data analysis. To this end, we present new theoretical results on the convergence of regularized Wasserstein estimators. We also study their numerical performances using simulated and real data in the supervised learning problem of proportions estimation in mixture models using optimal transport.