$h$-analysis and data-parallel physics-informed neural networks

We explore the data-parallel acceleration of physics-informed machine learning (PIML) schemes, with a focus on physics-informed neural networks (PINNs) for multiple graphics processing units (GPUs) architectures. In order to develop scale-robust PIML models for sophisticated applications (e.g., involving complex and high-dimensional domains, non-linear operators or multi-physics), which may require a large number of training points, we detail a protocol based on the Horovod training framework. This protocol is backed by $h$-analysis, including a new convergence bound for the generalization error. We show that the acceleration is straightforward to implement, does not compromise training, and proves to be highly efficient, paving the way towards generic scale-robust PIML. Extensive numerical experiments with increasing complexity illustrate its robustness and consistency, offering a wide range of possibilities for real-world simulations.

Physics-informed neural networks for operator equations with stochastic data

We consider the computation of statistical moments to operator equations with stochastic data. We remark that application of PINNs -- referred to as TPINNs -- allows to solve the induced tensor operator equations under minimal changes of existing PINNs code. This scheme can overcome the curse of dimensionality and covers non-linear and time-dependent operators. We propose two types of architectures, referred to as vanilla and multi-output TPINNs, and investigate their benefits and limitations. Exhaustive numerical experiments are performed; demonstrating applicability and performance; raising a variety of new promising research avenues.

Hyper-parameter tuning of physics-informed neural networks: Application to Helmholtz problems

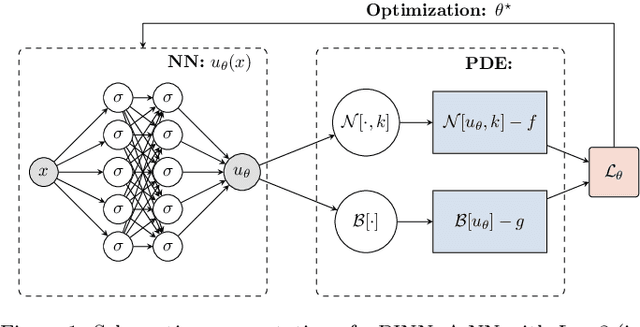
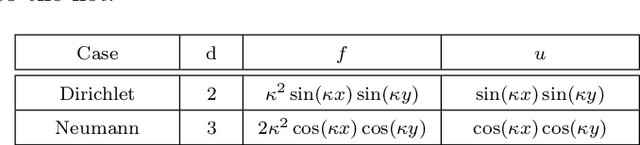
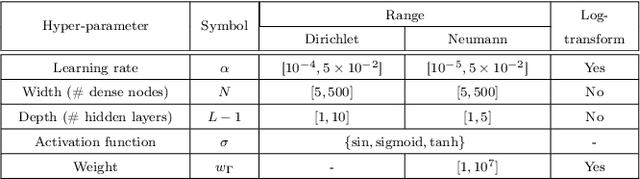
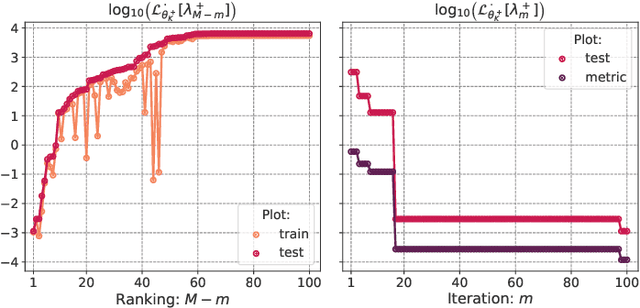
We consider physics-informed neural networks [Raissi et al., J. Comput. Phys. 278 (2019) 686-707] for forward physical problems. In order to find optimal PINNs configuration, we introduce a hyper-parameter tuning procedure via Gaussian processes-based Bayesian optimization. We apply the procedure to Helmholtz problems for bounded domains and conduct a thorough study, focusing on: (i) performance, (ii) the collocation points density $r$ and (iii) the frequency $\kappa$, confirming the applicability and necessity of the method. Numerical experiments are performed in two and three dimensions, including comparison to finite element methods.