The Price of Local Fairness in Multistage Selection

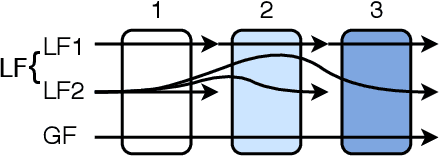
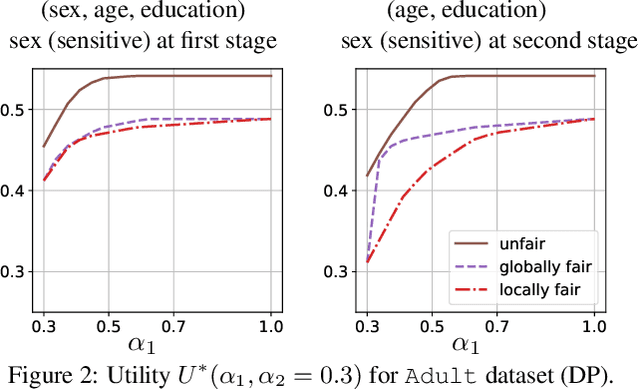
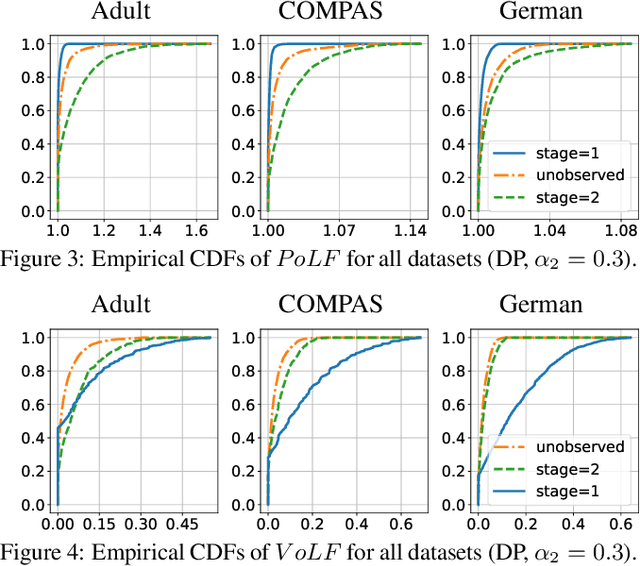
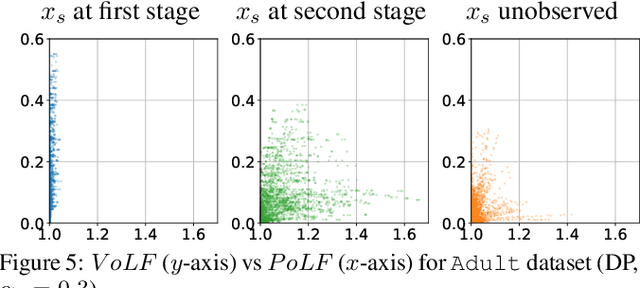
The rise of algorithmic decision making led to active researches on how to define and guarantee fairness, mostly focusing on one-shot decision making. In several important applications such as hiring, however, decisions are made in multiple stage with additional information at each stage. In such cases, fairness issues remain poorly understood. In this paper we study fairness in $k$-stage selection problems where additional features are observed at every stage. We first introduce two fairness notions, local (per stage) and global (final stage) fairness, that extend the classical fairness notions to the $k$-stage setting. We propose a simple model based on a probabilistic formulation and show that the locally and globally fair selections that maximize precision can be computed via a linear program. We then define the price of local fairness to measure the loss of precision induced by local constraints; and investigate theoretically and empirically this quantity. In particular, our experiments show that the price of local fairness is generally smaller when the sensitive attribute is observed at the first stage; but globally fair selections are more locally fair when the sensitive attribute is observed at the second stage---hence in both cases it is often possible to have a selection that has a small price of local fairness and is close to locally fair.

Colonel Blotto and Hide-and-Seek Games as Path Planning Problems with Side Observations

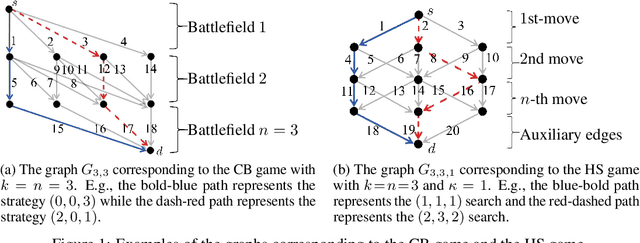
Resource allocation games such as the famous Colonel Blotto (CB) and Hide-and-Seek (HS) games are often used to model a large variety of practical problems, but only in their one-shot versions. Indeed, due to their extremely large strategy space, it remains an open question how one can efficiently learn in these games. In this work, we show that the online CB and HS games can be cast as path planning problems with side-observations (SOPPP): at each stage, a learner chooses a path on a directed acyclic graph and suffers the sum of losses that are adversarially assigned to the corresponding edges; and she then receives semi-bandit feedback with side-observations (i.e., she observes the losses on the chosen edges plus some others). Then, we propose a novel algorithm, EXP3-OE, the first-of-its-kind with guaranteed efficient running time for SOPPP without requiring any auxiliary oracle. We provide an expected-regret bound of EXP3-OE in SOPPP matching the order of the best benchmark in the literature. Moreover, we introduce additional assumptions on the observability model under which we can further improve the regret bounds of EXP3-OE. We illustrate the benefit of using EXP3-OE in SOPPP by applying it to the online CB and HS games.

An Approximate Dynamic Programming Approach to Repeated Games with Vector Losses

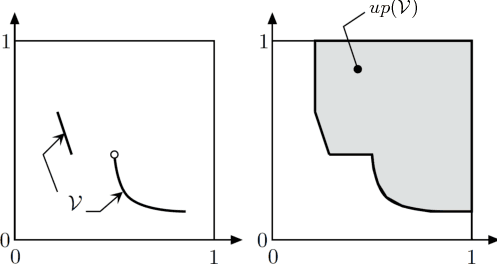
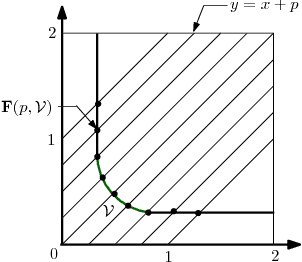
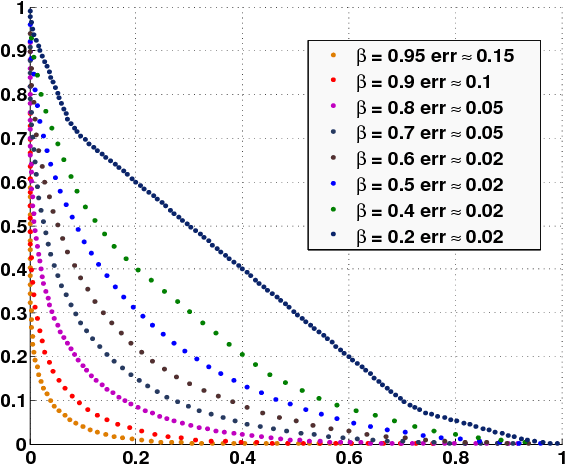
We describe an approximate dynamic programming (ADP) approach to compute approximately optimal strategies and approximations of the minimal losses that can be guaranteed in discounted repeated games with vector losses. At the core of our approach is a characterization of the lower Pareto frontier of the set of expected losses that a player can guarantee in these games as the unique fixed point of a set-valued dynamic programming (DP) operator. This fixed point can be approximated by an iterative application of this DP operator compounded by a polytopic set approximation, beginning with a single point. Each iteration can be computed by solving a set of linear programs corresponding to the vertices of the polytope. We derive rigorous bounds on the error of the resulting approximation and the performance of the corresponding approximately optimal strategies. We discuss an application to regret minimization in repeated decision-making in adversarial environments, where we show that this approach can be used to compute approximately optimal strategies and approximations of the minimax optimal regret when the action sets are finite. We illustrate this approach by computing provably approximately optimal strategies for the problem of prediction using expert advice under discounted $\{0,1\}-$losses. Our numerical evaluations demonstrate the sub-optimality of well-known off-the-shelf online learning algorithms like Hedge and a significantly improved performance on using our approximately optimal strategies in these settings. Our work thus demonstrates the significant potential in using the ADP framework to design effective online learning algorithms.

Linear Regression as a Non-Cooperative Game

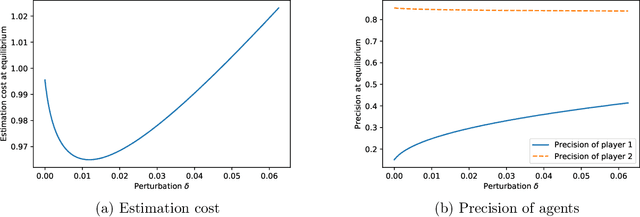
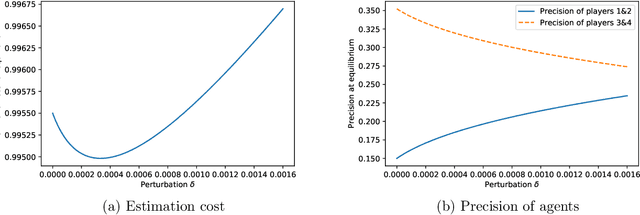
Linear regression amounts to estimating a linear model that maps features (e.g., age or gender) to corresponding data (e.g., the answer to a survey or the outcome of a medical exam). It is a ubiquitous tool in experimental sciences. We study a setting in which features are public but the data is private information. While the estimation of the linear model may be useful to participating individuals, (if, e.g., it leads to the discovery of a treatment to a disease), individuals may be reluctant to disclose their data due to privacy concerns. In this paper, we propose a generic game-theoretic model to express this trade-off. Users add noise to their data before releasing it. In particular, they choose the variance of this noise to minimize a cost comprising two components: (a) a privacy cost, representing the loss of privacy incurred by the release; and (b) an estimation cost, representing the inaccuracy in the linear model estimate. We study the Nash equilibria of this game, establishing the existence of a unique non-trivial equilibrium. We determine its efficiency for several classes of privacy and estimation costs, using the concept of the price of stability. Finally, we prove that, for a specific estimation cost, the generalized least-square estimator is optimal among all linear unbiased estimators in our non-cooperative setting: this result extends the famous Aitken/Gauss-Markov theorem in statistics, establishing that its conclusion persists even in the presence of strategic individuals.