A Universal Nearest-Neighbor Estimator for Intrinsic Dimensionality

Estimating the intrinsic dimensionality (ID) of data is a fundamental problem in machine learning and computer vision, providing insight into the true degrees of freedom underlying high-dimensional observations. Existing methods often rely on geometric or distributional assumptions and can significantly fail when these assumptions are violated. In this paper, we introduce a novel ID estimator based on nearest-neighbor distance ratios that involves simple calculations and achieves state-of-the-art results. Most importantly, we provide a theoretical analysis proving that our estimator is \emph{universal}, namely, it converges to the true ID independently of the distribution generating the data. We present experimental results on benchmark manifolds and real-world datasets to demonstrate the performance of our estimator.

Joint Geometric and Topological Analysis of Hierarchical Datasets

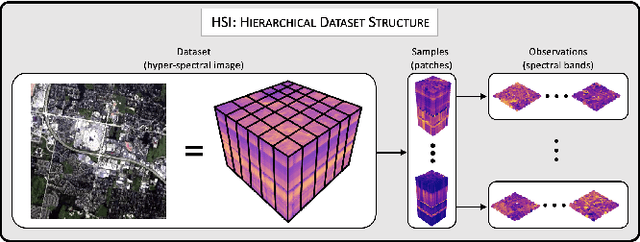
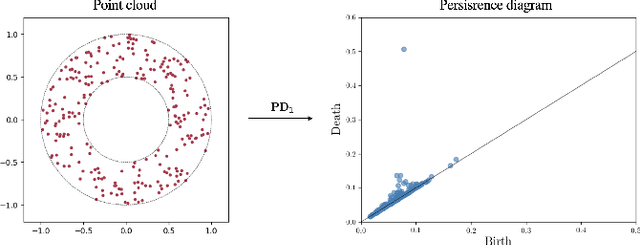
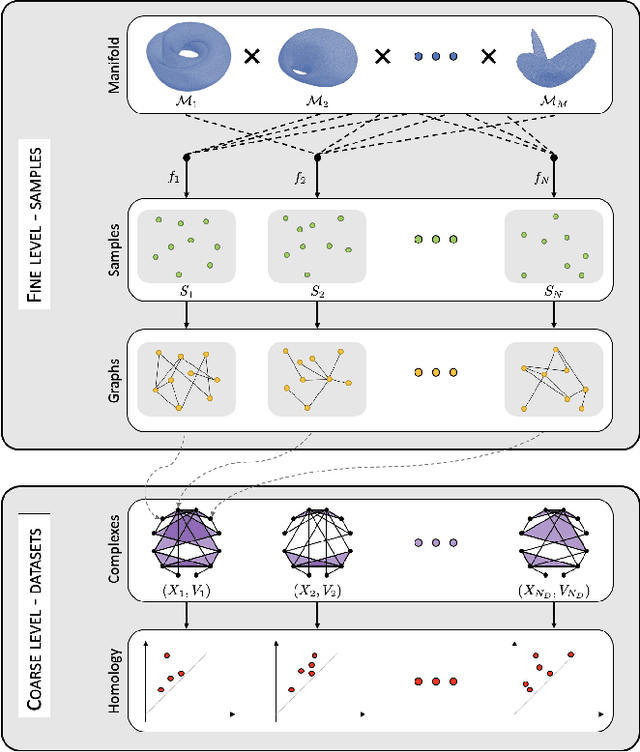
In a world abundant with diverse data arising from complex acquisition techniques, there is a growing need for new data analysis methods. In this paper we focus on high-dimensional data that are organized into several hierarchical datasets. We assume that each dataset consists of complex samples, and every sample has a distinct irregular structure modeled by a graph. The main novelty in this work lies in the combination of two complementing powerful data-analytic approaches: topological data analysis (TDA) and geometric manifold learning. Geometry primarily contains local information, while topology inherently provides global descriptors. Based on this combination, we present a method for building an informative representation of hierarchical datasets. At the finer (sample) level, we devise a new metric between samples based on manifold learning that facilitates quantitative structural analysis. At the coarser (dataset) level, we employ TDA to extract qualitative structural information from the datasets. We showcase the applicability and advantages of our method on simulated data and on a corpus of hyper-spectral images. We show that an ensemble of hyper-spectral images exhibits a hierarchical structure that fits well the considered setting. In addition, we show that our new method gives rise to superior classification results compared to state-of-the-art methods.

Cycle Registration in Persistent Homology with Applications in Topological Bootstrap

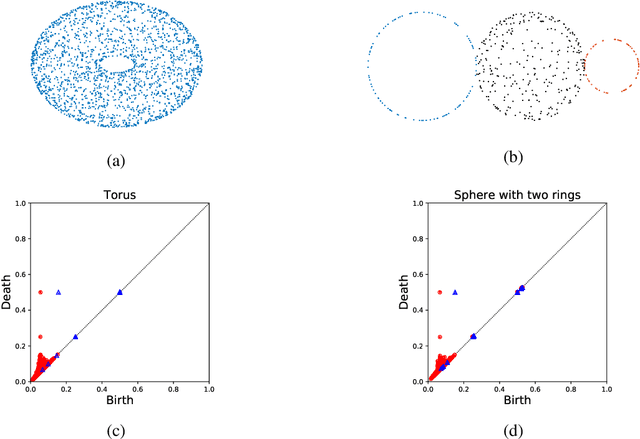
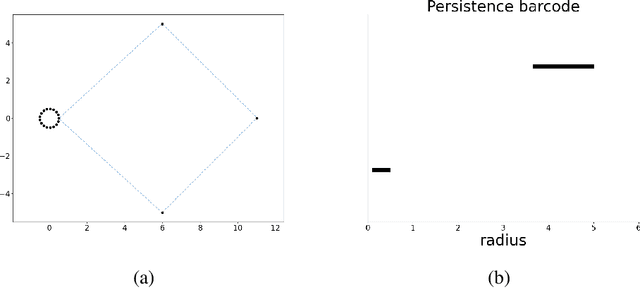
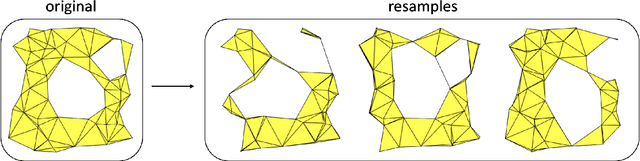
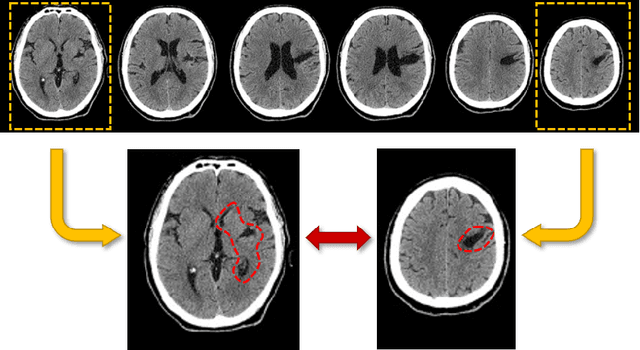
In this article we propose a novel approach for comparing the persistent homology representations of two spaces (filtrations). Commonly used methods are based on numerical summaries such as persistence diagrams and persistence landscapes, along with suitable metrics (e.g. Wasserstein). These summaries are useful for computational purposes, but they are merely a marginal of the actual topological information that persistent homology can provide. Instead, our approach compares between two topological representations directly in the data space. We do so by defining a correspondence relation between individual persistent cycles of two different spaces, and devising a method for computing this correspondence. Our matching of cycles is based on both the persistence intervals and the spatial placement of each feature. We demonstrate our new framework in the context of topological inference, where we use statistical bootstrap methods in order to differentiate between real features and noise in point cloud data.