Operator Calculus for Population-Based Optimization: A Mean-Field Convergence Theory

Population-based and distributional optimization methods, from evolution strategies and consensus-based optimization to covariance-matrix adaptation and stochastic gradient methods viewed as distributional dynamics, are widely used for nonconvex or black-box problems, yet their convergence analyses remain fragmented across algorithm-specific techniques. We introduce an operator calculus in which a broad class of such methods, after choosing an appropriate state space and, where necessary, augmenting the state by memory or strategy variables, is described as a composition of three elementary operators (mutation, selection, and recombination) acting on probability measures. Under explicit stability and regularity conditions, the composite operator admits a pre-generator whose continuous-time limit is a transport-reaction-jump (TRJ) PDE that preserves the operator splitting. On this foundation we establish a modular Lyapunov principle. If a state-space Lyapunov function both dissipates under the full generator and controls the relevant search-space gauges, then the state-space Lyapunov functional and the induced search errors decay exponentially. The additive generator structure allows dissipation estimates to be assembled operator by operator, providing a toolkit for certifying convergence of composite mean-field algorithms.

Convex Regularization and Convergence of Policy Gradient Flows under Safety Constraints

This paper studies reinforcement learning (RL) in infinite-horizon dynamic decision processes with almost-sure safety constraints. Such safety-constrained decision processes are central to applications in autonomous systems, finance, and resource management, where policies must satisfy strict, state-dependent constraints. We consider a doubly-regularized RL framework that combines reward and parameter regularization to address these constraints within continuous state-action spaces. Specifically, we formulate the problem as a convex regularized objective with parametrized policies in the mean-field regime. Our approach leverages recent developments in mean-field theory and Wasserstein gradient flows to model policies as elements of an infinite-dimensional statistical manifold, with policy updates evolving via gradient flows on the space of parameter distributions. Our main contributions include establishing solvability conditions for safety-constrained problems, defining smooth and bounded approximations that facilitate gradient flows, and demonstrating exponential convergence towards global solutions under sufficient regularization. We provide general conditions on regularization functions, encompassing standard entropy regularization as a special case. The results also enable a particle method implementation for practical RL applications. The theoretical insights and convergence guarantees presented here offer a robust framework for safe RL in complex, high-dimensional decision-making problems.

Optimal Management of Naturally Regenerating Uneven-aged Forests

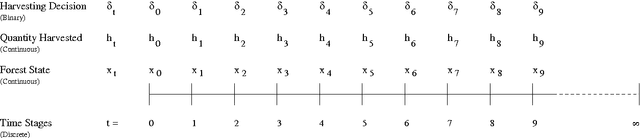
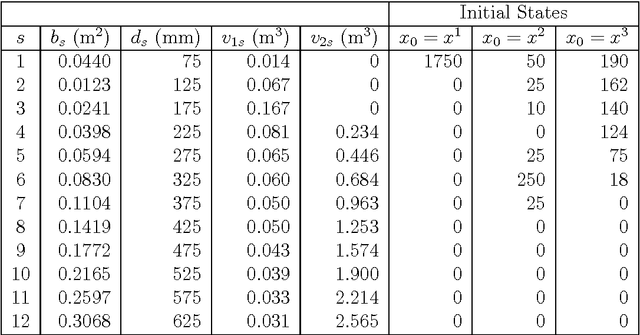
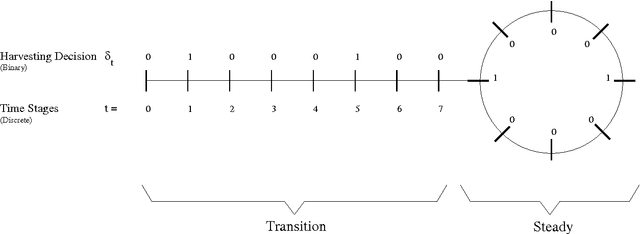
A shift from even-aged forest management to uneven-aged management practices leads to a problem rather different from the existing straightforward practice that follows a rotation cycle of artificial regeneration, thinning of inferior trees and a clearcut. A lack of realistic models and methods suggesting how to manage uneven-aged stands in a way that is economically viable and ecologically sustainable creates difficulties in adopting this new management practice. To tackle this problem, we make a two-fold contribution in this paper. The first contribution is the proposal of an algorithm that is able to handle a realistic uneven-aged stand management model that is otherwise computationally tedious and intractable. The model considered in this paper is an empirically estimated size-structured ecological model for uneven-aged spruce forests. The second contribution is on the sensitivity analysis of the forest model with respect to a number of important parameters. The analysis provides us an insight into the behavior of the uneven-aged forest model.