Bidirectional Variational Autoencoders

We present the new bidirectional variational autoencoder (BVAE) network architecture. The BVAE uses a single neural network both to encode and decode instead of an encoder-decoder network pair. The network encodes in the forward direction and decodes in the backward direction through the same synaptic web. Simulations compared BVAEs and ordinary VAEs on the four image tasks of image reconstruction, classification, interpolation, and generation. The image datasets included MNIST handwritten digits, Fashion-MNIST, CIFAR-10, and CelebA-64 face images. The bidirectional structure of BVAEs cut the parameter count by almost 50% and still slightly outperformed the unidirectional VAEs.

Training Deep Neural Classifiers with Soft Diamond Regularizers

We introduce new \emph{soft diamond} regularizers that both improve synaptic sparsity and maintain classification accuracy in deep neural networks. These parametrized regularizers outperform the state-of-the-art hard-diamond Laplacian regularizer of Lasso regression and classification. They use thick-tailed symmetric alpha-stable ($\mathcal{S \alpha S}$) bell-curve synaptic weight priors that are not Gaussian and so have thicker tails. The geometry of the diamond-shaped constraint set varies from a circle to a star depending on the tail thickness and dispersion of the prior probability density function. Training directly with these priors is computationally intensive because almost all $\mathcal{S \alpha S}$ probability densities lack a closed form. A precomputed look-up table removed this computational bottleneck. We tested the new soft diamond regularizers with deep neural classifiers on the three datasets CIFAR-10, CIFAR-100, and Caltech-256. The regularizers improved the accuracy of the classifiers. The improvements included $4.57\%$ on CIFAR-10, $4.27\%$ on CIFAR-100, and $6.69\%$ on Caltech-256. They also outperformed $L_2$ regularizers on all the test cases. Soft diamond regularizers also outperformed $L_1$ lasso or Laplace regularizers because they better increased sparsity while improving classification accuracy. Soft-diamond priors substantially improved accuracy on CIFAR-10 when combined with dropout, batch, or data-augmentation regularization.

Optimizing Black-box Metrics with Adaptive Surrogates

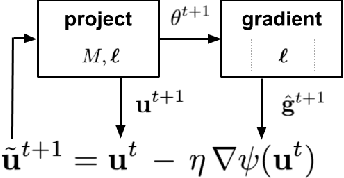
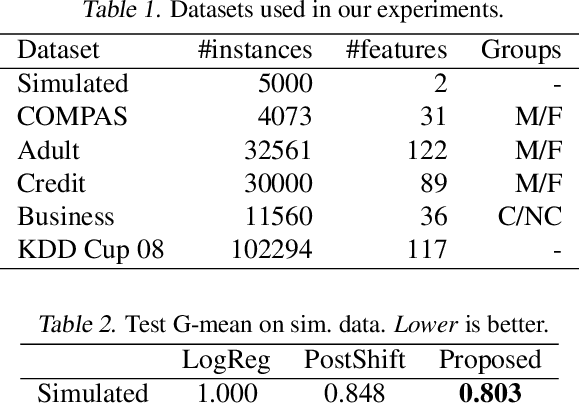
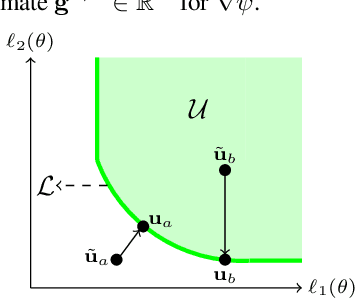
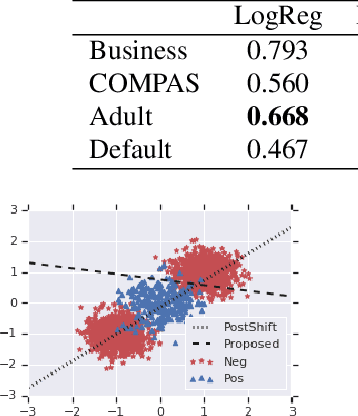
We address the problem of training models with black-box and hard-to-optimize metrics by expressing the metric as a monotonic function of a small number of easy-to-optimize surrogates. We pose the training problem as an optimization over a relaxed surrogate space, which we solve by estimating local gradients for the metric and performing inexact convex projections. We analyze gradient estimates based on finite differences and local linear interpolations, and show convergence of our approach under smoothness assumptions with respect to the surrogates. Experimental results on classification and ranking problems verify the proposal performs on par with methods that know the mathematical formulation, and adds notable value when the form of the metric is unknown.