The Connection Between Approximation, Depth Separation and Learnability in Neural Networks

Several recent works have shown separation results between deep neural networks, and hypothesis classes with inferior approximation capacity such as shallow networks or kernel classes. On the other hand, the fact that deep networks can efficiently express a target function does not mean this target function can be learned efficiently by deep neural networks. In this work we study the intricate connection between learnability and approximation capacity. We show that learnability with deep networks of a target function depends on the ability of simpler classes to approximate the target. Specifically, we show that a necessary condition for a function to be learnable by gradient descent on deep neural networks is to be able to approximate the function, at least in a weak sense, with shallow neural networks. We also show that a class of functions can be learned by an efficient statistical query algorithm if and only if it can be approximated in a weak sense by some kernel class. We give several examples of functions which demonstrate depth separation, and conclude that they cannot be efficiently learned, even by a hypothesis class that can efficiently approximate them.

Implicit Regularization in ReLU Networks with the Square Loss

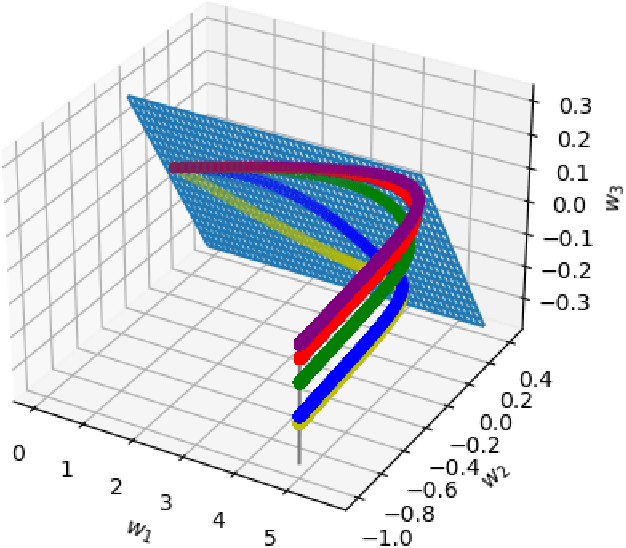
Understanding the implicit regularization (or implicit bias) of gradient descent has recently been a very active research area. However, the implicit regularization in nonlinear neural networks is still poorly understood, especially for regression losses such as the square loss. Perhaps surprisingly, we prove that even for a single ReLU neuron, it is impossible to characterize the implicit regularization with the square loss by any explicit function of the model parameters (although on the positive side, we show it can be characterized approximately). For one hidden-layer networks, we prove a similar result, where in general it is impossible to characterize implicit regularization properties in this manner, except for the "balancedness" property identified in Du et al. [2018]. Our results suggest that a more general framework than the one considered so far may be needed to understand implicit regularization for nonlinear predictors, and provides some clues on what this framework should be.

High-Order Oracle Complexity of Smooth and Strongly Convex Optimization

In this note, we consider the complexity of optimizing a highly smooth (Lipschitz $k$-th order derivative) and strongly convex function, via calls to a $k$-th order oracle which returns the value and first $k$ derivatives of the function at a given point, and where the dimension is unrestricted. Extending the techniques introduced in Arjevani et al. [2019], we prove that the worst-case oracle complexity for any fixed $k$ to optimize the function up to accuracy $\epsilon$ is on the order of $\left(\frac{\mu_k D^{k-1}}{\lambda}\right)^{\frac{2}{3k+1}}+\log\log\left(\frac{1}{\epsilon}\right)$ (up to log factors independent of $\epsilon$), where $\mu_k$ is the Lipschitz constant of the $k$-th derivative, $D$ is the initial distance to the optimum, and $\lambda$ is the strong convexity parameter.

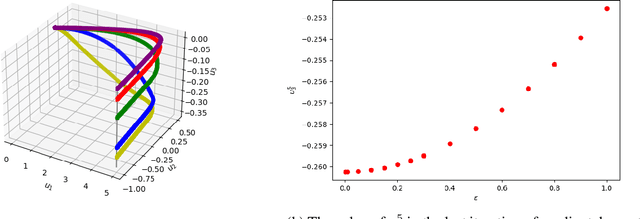
Gradient Methods Never Overfit On Separable Data

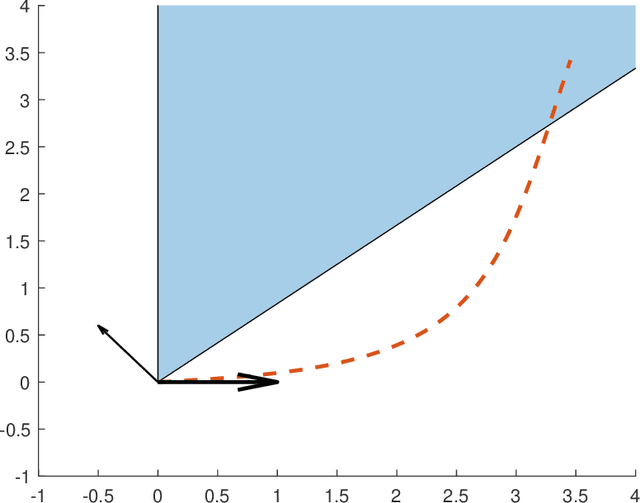
A line of recent works established that when training linear predictors over separable data, using gradient methods and exponentially-tailed losses, the predictors asymptotically converge in direction to the max-margin predictor. As a consequence, the predictors asymptotically do not overfit. However, this does not address the question of whether overfitting might occur non-asymptotically, after some bounded number of iterations. In this paper, we formally show that standard gradient methods (in particular, gradient flow, gradient descent and stochastic gradient descent) never overfit on separable data: If we run these methods for $T$ iterations on a dataset of size $m$, both the empirical risk and the generalization error decrease at an essentially optimal rate of $\tilde{\mathcal{O}}(1/\gamma^2 T)$ up till $T\approx m$, at which point the generalization error remains fixed at an essentially optimal level of $\tilde{\mathcal{O}}(1/\gamma^2 m)$ regardless of how large $T$ is. Along the way, we present non-asymptotic bounds on the number of margin violations over the dataset, and prove their tightness.

Neural Networks with Small Weights and Depth-Separation Barriers

In studying the expressiveness of neural networks, an important question is whether there are functions which can only be approximated by sufficiently deep networks, assuming their size is bounded. However, for constant depths, existing results are limited to depths $2$ and $3$, and achieving results for higher depths has been an important open question. In this paper, we focus on feedforward ReLU networks, and prove fundamental barriers to proving such results beyond depth $4$, by reduction to open problems and natural-proof barriers in circuit complexity. To show this, we study a seemingly unrelated problem of independent interest: Namely, whether there are polynomially-bounded functions which require super-polynomial weights in order to approximate with constant-depth neural networks. We provide a negative and constructive answer to that question, by showing that if a function can be approximated by a polynomially-sized, constant depth $k$ network with arbitrarily large weights, it can also be approximated by a polynomially-sized, depth $3k+3$ network, whose weights are polynomially bounded.

The Effects of Mild Over-parameterization on the Optimization Landscape of Shallow ReLU Neural Networks

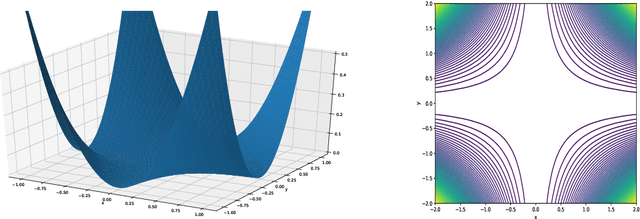
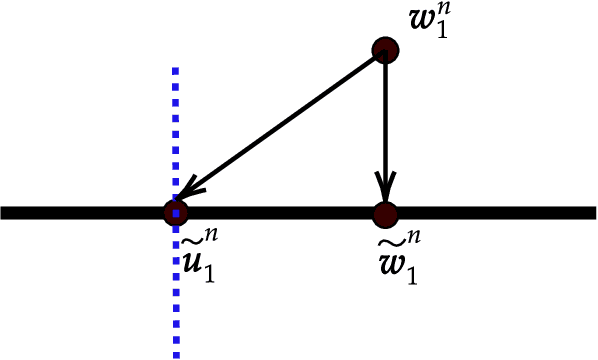
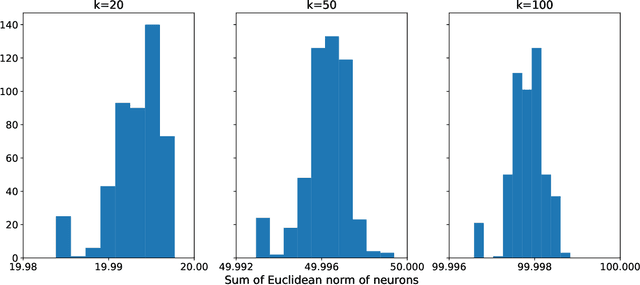
We study the effects of mild over-parameterization on the optimization landscape of a simple ReLU neural network of the form $\mathbf{x}\mapsto\sum_{i=1}^k\max\{0,\mathbf{w}_i^{\top}\mathbf{x}\}$, in a well-studied teacher-student setting where the target values are generated by the same architecture, and when directly optimizing over the population squared loss with respect to Gaussian inputs. We prove that while the objective is strongly convex around the global minima when the teacher and student networks possess the same number of neurons, it is not even \emph{locally convex} after any amount of over-parameterization. Moreover, related desirable properties (e.g., one-point strong convexity and the Polyak-{\L}ojasiewicz condition) also do not hold even locally. On the other hand, we establish that the objective remains one-point strongly convex in \emph{most} directions (suitably defined). For the non-global minima, we prove that adding even just a single neuron will turn a non-global minimum into a saddle point. This holds under some technical conditions which we validate empirically. These results provide a possible explanation for why recovering a global minimum becomes significantly easier when we over-parameterize, even if the amount of over-parameterization is very moderate.

Can We Find Near-Approximately-Stationary Points of Nonsmooth Nonconvex Functions?

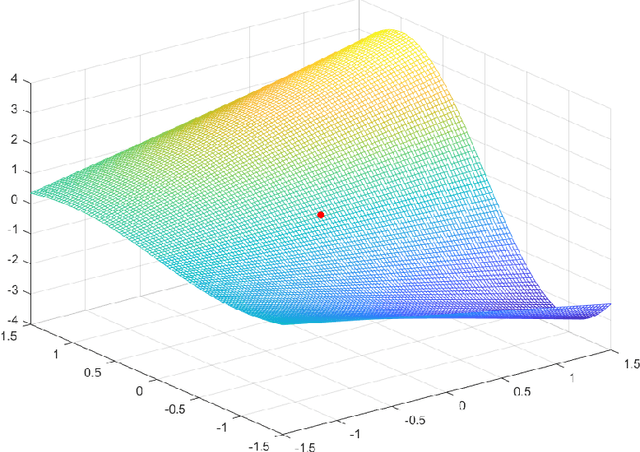
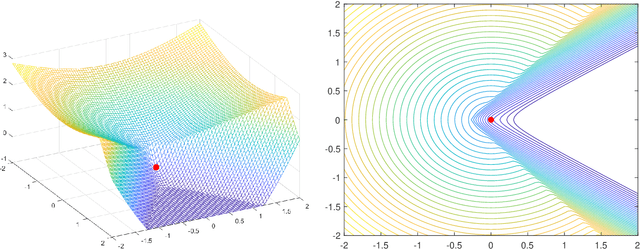
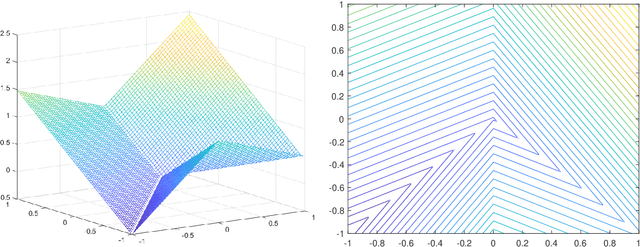
It is well-known that given a bounded, smooth nonconvex function, standard gradient-based methods can find $\epsilon$-stationary points (where the gradient norm is less than $\epsilon$) in $\mathcal{O}(1/\epsilon^2)$ iterations. However, many important nonconvex optimization problems, such as those associated with training modern neural networks, are inherently not smooth, making these results inapplicable. Moreover, as recently pointed out in Zhang et al. [2020], it is generally impossible to provide finite-time guarantees for finding an $\epsilon$-stationary point of nonsmooth functions. Perhaps the most natural relaxation of this is to find points which are near such $\epsilon$-stationary points. In this paper, we show that even this relaxed goal is hard to obtain in general, given only black-box access to the function values and gradients. We also discuss the pros and cons of alternative approaches.

Is Local SGD Better than Minibatch SGD?

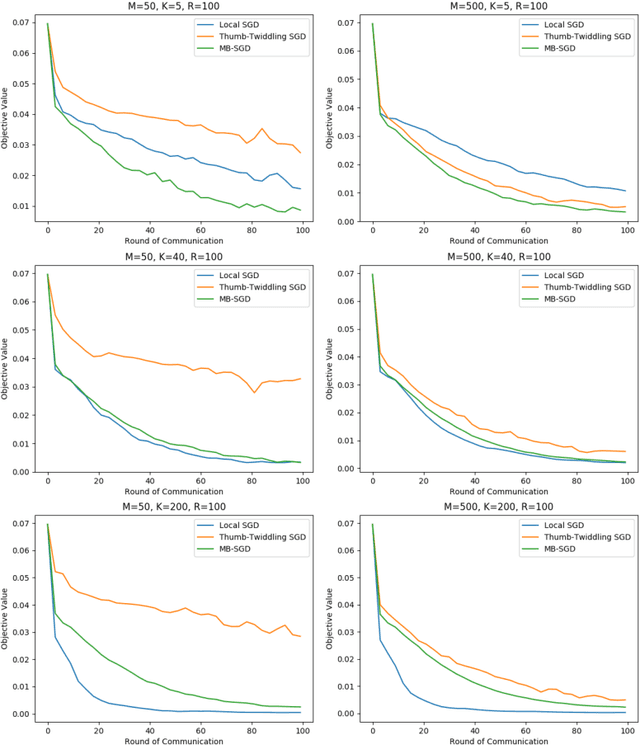
We study local SGD (also known as parallel SGD and federated averaging), a natural and frequently used stochastic distributed optimization method. Its theoretical foundations are currently lacking and we highlight how all existing error guarantees in the convex setting are dominated by a simple baseline, minibatch SGD. (1) For quadratic objectives we prove that local SGD strictly dominates minibatch SGD and that accelerated local SGD is minimax optimal for quadratics; (2) For general convex objectives we provide the first guarantee that at least sometimes improves over minibatch SGD; (3) We show that indeed local SGD does not dominate minibatch SGD by presenting a lower bound on the performance of local SGD that is worse than the minibatch SGD guarantee.

Learning a Single Neuron with Gradient Methods

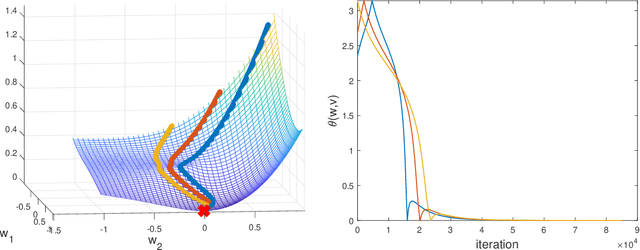
We consider the fundamental problem of learning a single neuron $x \mapsto\sigma(w^\top x)$ using standard gradient methods. As opposed to previous works, which considered specific (and not always realistic) input distributions and activation functions $\sigma(\cdot)$, we ask whether a more general result is attainable, under milder assumptions. On the one hand, we show that some assumptions on the distribution and the activation function are necessary. On the other hand, we prove positive guarantees under mild assumptions, which go beyond those studied in the literature so far. We also point out and study the challenges in further strengthening and generalizing our results.

Proving the Lottery Ticket Hypothesis: Pruning is All You Need

The lottery ticket hypothesis (Frankle and Carbin, 2018), states that a randomly-initialized network contains a small subnetwork such that, when trained in isolation, can compete with the performance of the original network. We prove an even stronger hypothesis (as was also conjectured in Ramanujan et al., 2019), showing that for every bounded distribution and every target network with bounded weights, a sufficiently over-parameterized neural network with random weights contains a subnetwork with roughly the same accuracy as the target network, without any further training.