When and how can inexact generative models still sample from the data manifold?

A curious phenomenon observed in some dynamical generative models is the following: despite learning errors in the score function or the drift vector field, the generated samples appear to shift \emph{along} the support of the data distribution but not \emph{away} from it. In this work, we investigate this phenomenon of \emph{robustness of the support} by taking a dynamical systems approach on the generating stochastic/deterministic process. Our perturbation analysis of the probability flow reveals that infinitesimal learning errors cause the predicted density to be different from the target density only on the data manifold for a wide class of generative models. Further, what is the dynamical mechanism that leads to the robustness of the support? We show that the alignment of the top Lyapunov vectors (most sensitive infinitesimal perturbation directions) with the tangent spaces along the boundary of the data manifold leads to robustness and prove a sufficient condition on the dynamics of the generating process to achieve this alignment. Moreover, the alignment condition is efficient to compute and, in practice, for robust generative models, automatically leads to accurate estimates of the tangent bundle of the data manifold. Using a finite-time linear perturbation analysis on samples paths as well as probability flows, our work complements and extends existing works on obtaining theoretical guarantees for generative models from a stochastic analysis, statistical learning and uncertainty quantification points of view. Our results apply across different dynamical generative models, such as conditional flow-matching and score-based generative models, and for different target distributions that may or may not satisfy the manifold hypothesis.

When are dynamical systems learned from time series data statistically accurate?

Conventional notions of generalization often fail to describe the ability of learned models to capture meaningful information from dynamical data. A neural network that learns complex dynamics with a small test error may still fail to reproduce its \emph{physical} behavior, including associated statistical moments and Lyapunov exponents. To address this gap, we propose an ergodic theoretic approach to generalization of complex dynamical models learned from time series data. Our main contribution is to define and analyze generalization of a broad suite of neural representations of classes of ergodic systems, including chaotic systems, in a way that captures emulating underlying invariant, physical measures. Our results provide theoretical justification for why regression methods for generators of dynamical systems (Neural ODEs) fail to generalize, and why their statistical accuracy improves upon adding Jacobian information during training. We verify our results on a number of ergodic chaotic systems and neural network parameterizations, including MLPs, ResNets, Fourier Neural layers, and RNNs.

A score-based operator Newton method for measure transport

Transportation of probability measures underlies many core tasks in statistics and machine learning, from variational inference to generative modeling. A typical goal is to represent a target probability measure of interest as the push-forward of a tractable source measure through a learned map. We present a new construction of such a transport map, given the ability to evaluate the score of the target distribution. Specifically, we characterize the map as a zero of an infinite-dimensional score-residual operator and derive a Newton-type method for iteratively constructing such a zero. We prove convergence of these iterations by invoking classical elliptic regularity theory for partial differential equations (PDE) and show that this construction enjoys rapid convergence, under smoothness assumptions on the target score. A key element of our approach is a generalization of the elementary Newton method to infinite-dimensional operators, other forms of which have appeared in nonlinear PDE and in dynamical systems. Our Newton construction, while developed in a functional setting, also suggests new iterative algorithms for approximating transport maps.

On the generalization of learning algorithms that do not converge

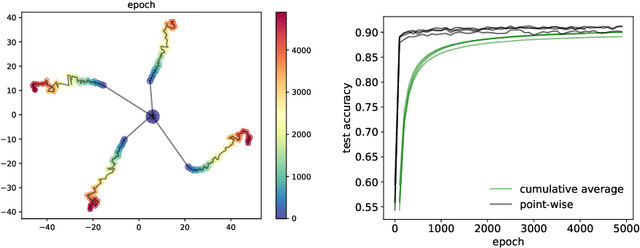
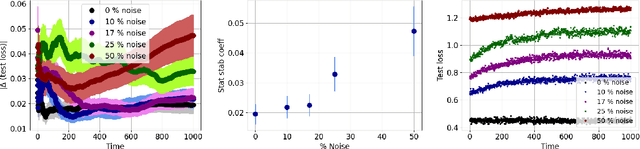
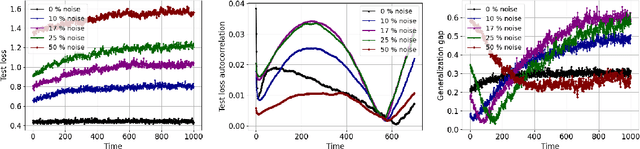
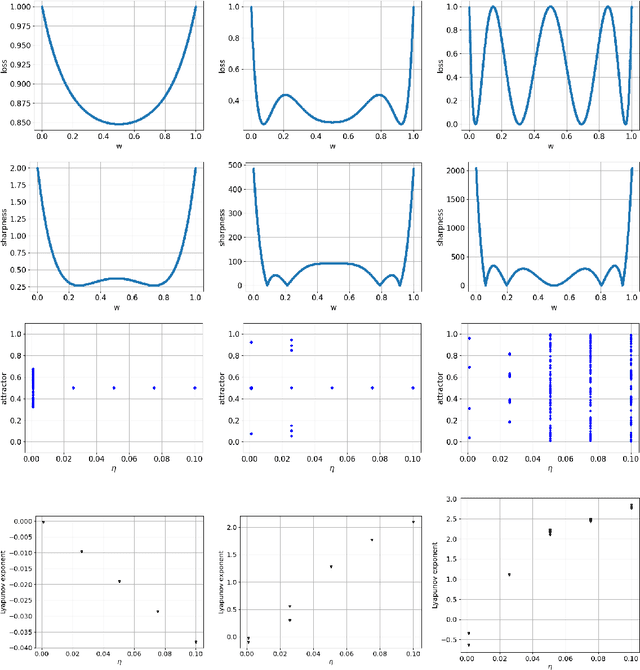
Generalization analyses of deep learning typically assume that the training converges to a fixed point. But, recent results indicate that in practice, the weights of deep neural networks optimized with stochastic gradient descent often oscillate indefinitely. To reduce this discrepancy between theory and practice, this paper focuses on the generalization of neural networks whose training dynamics do not necessarily converge to fixed points. Our main contribution is to propose a notion of statistical algorithmic stability (SAS) that extends classical algorithmic stability to non-convergent algorithms and to study its connection to generalization. This ergodic-theoretic approach leads to new insights when compared to the traditional optimization and learning theory perspectives. We prove that the stability of the time-asymptotic behavior of a learning algorithm relates to its generalization and empirically demonstrate how loss dynamics can provide clues to generalization performance. Our findings provide evidence that networks that "train stably generalize better" even when the training continues indefinitely and the weights do not converge.