Exact Learning Dynamics of In-Context Learning in Linear Transformers and Its Application to Non-Linear Transformers

Transformer models exhibit remarkable in-context learning (ICL), adapting to novel tasks from examples within their context, yet the underlying mechanisms remain largely mysterious. Here, we provide an exact analytical characterization of ICL emergence by deriving the closed-form stochastic gradient descent (SGD) dynamics for a simplified linear transformer performing regression tasks. Our analysis reveals key properties: (1) a natural separation of timescales directly governed by the input data's covariance structure, leading to staged learning; (2) an exact description of how ICL develops, including fixed points corresponding to learned algorithms and conservation laws constraining the dynamics; and (3) surprisingly nonlinear learning behavior despite the model's linearity. We hypothesize this phenomenology extends to non-linear models. To test this, we introduce theory-inspired macroscopic measures (spectral rank dynamics, subspace stability) and use them to provide mechanistic explanations for (1) the sudden emergence of ICL in attention-only networks and (2) delayed generalization (grokking) in modular arithmetic models. Our work offers an exact dynamical model for ICL and theoretically grounded tools for analyzing complex transformer training.

Well, how accurate is it? A Study of Deep Learning Methods for Reynolds-Averaged Navier-Stokes Simulations

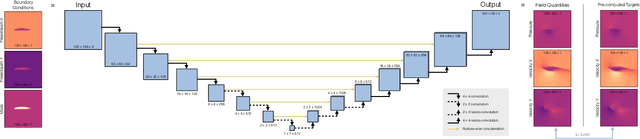
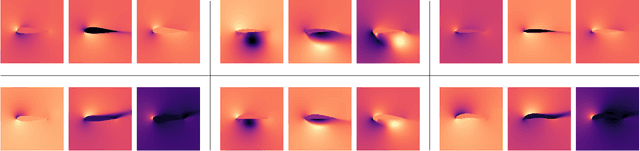
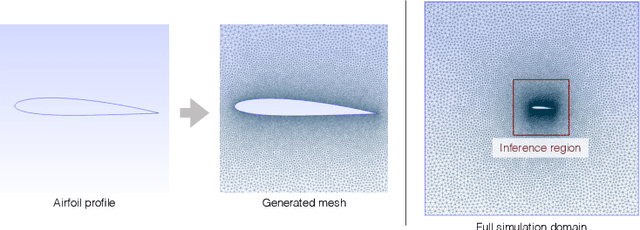
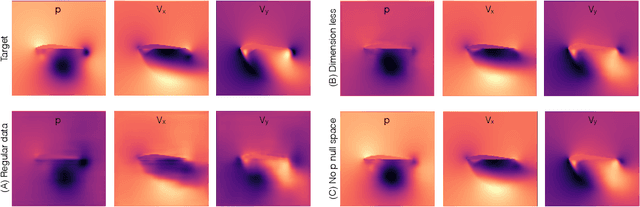
With this study we investigate the accuracy of deep learning models for the inference of Reynolds-Averaged Navier-Stokes solutions. We focus on a modernized U-net architecture, and evaluate a large number of trained neural networks with respect to their accuracy for the calculation of pressure and velocity distributions. In particular, we illustrate how training data size and the number of weights influence the accuracy of the solutions. With our best models we arrive at a mean relative pressure and velocity error of less than 3% across a range of previously unseen airfoil shapes. In addition all source code is publicly available in order to ensure reproducibility and to provide a starting point for researchers interested in deep learning methods for physics problems. While this work focuses on RANS solutions, the neural network architecture and learning setup are very generic, and applicable to a wide range of PDE boundary value problems on Cartesian grids.