Efficient Bayesian travel-time tomography with geologically-complex priors using sensitivity-informed polynomial chaos expansion and deep generative networks

Monte Carlo Markov Chain (MCMC) methods commonly confront two fundamental challenges: the accurate characterization of the prior distribution and the efficient evaluation of the likelihood. In the context of Bayesian studies on tomography, principal component analysis (PCA) can in some cases facilitate the straightforward definition of the prior distribution, while simultaneously enabling the implementation of accurate surrogate models based on polynomial chaos expansion (PCE) to replace computationally intensive full-physics forward solvers. When faced with scenarios where PCA does not offer a direct means of easily defining the prior distribution alternative methods like deep generative models (e.g., variational autoencoders (VAEs)), can be employed as viable options. However, accurately producing a surrogate capable of capturing the intricate non-linear relationship between the latent parameters of a VAE and the outputs of forward modeling presents a notable challenge. Indeed, while PCE models provide high accuracy when the input-output relationship can be effectively approximated by relatively low-degree multivariate polynomials, this condition is typically unmet when utilizing latent variables derived from deep generative models. In this contribution, we present a strategy that combines the excellent reconstruction performances of VAE in terms of prio representation with the accuracy of PCA-PCE surrogate modeling in the context of Bayesian ground penetrating radar (GPR) travel-time tomography. Within the MCMC process, the parametrization of the VAE is leveraged for prior exploration and sample proposal. Concurrently, modeling is conducted using PCE, which operates on either globally or locally defined principal components of the VAE samples under examination.

Uncertainty Quantification and Experimental Design for large-scale linear Inverse Problems under Gaussian Process Priors

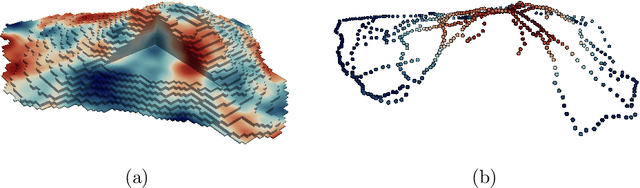
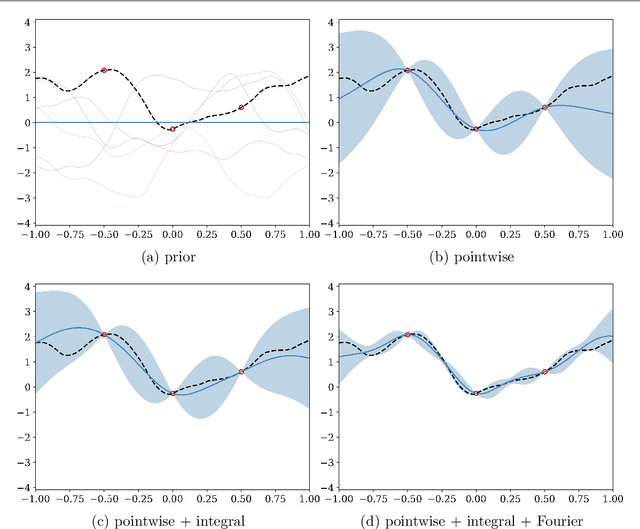
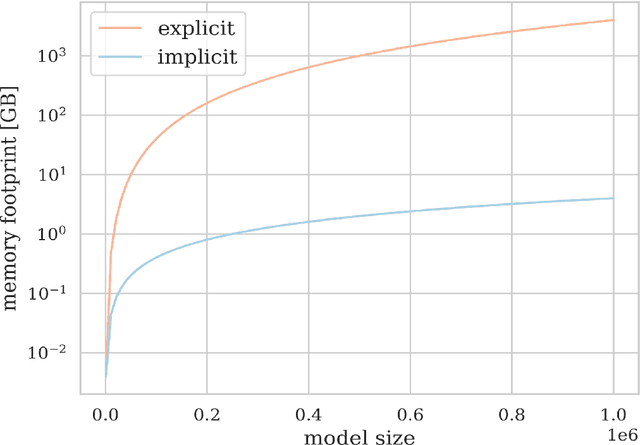
We consider the use of Gaussian process (GP) priors for solving inverse problems in a Bayesian framework. As is well known, the computational complexity of GPs scales cubically in the number of datapoints. We here show that in the context of inverse problems involving integral operators, one faces additional difficulties that hinder inversion on large grids. Furthermore, in that context, covariance matrices can become too large to be stored. By leveraging results about sequential disintegrations of Gaussian measures, we are able to introduce an implicit representation of posterior covariance matrices that reduces the memory footprint by only storing low rank intermediate matrices, while allowing individual elements to be accessed on-the-fly without needing to build full posterior covariance matrices. Moreover, it allows for fast sequential inclusion of new observations. These features are crucial when considering sequential experimental design tasks. We demonstrate our approach by computing sequential data collection plans for excursion set recovery for a gravimetric inverse problem, where the goal is to provide fine resolution estimates of high density regions inside the Stromboli volcano, Italy. Sequential data collection plans are computed by extending the weighted integrated variance reduction (wIVR) criterion to inverse problems. Our results show that this criterion is able to significantly reduce the uncertainty on the excursion volume, reaching close to minimal levels of residual uncertainty. Overall, our techniques allow the advantages of probabilistic models to be brought to bear on large-scale inverse problems arising in the natural sciences.

Fast ABC with joint generative modelling and subset simulation

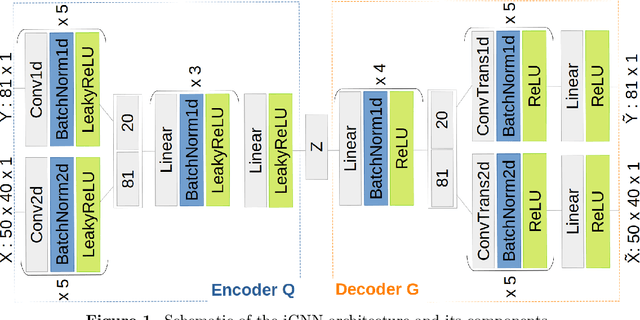
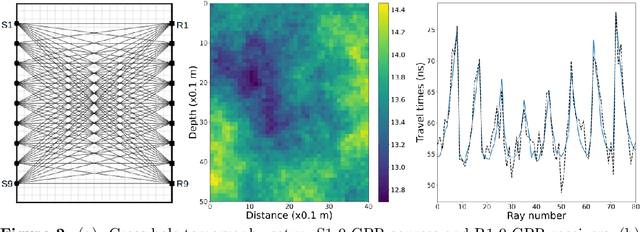
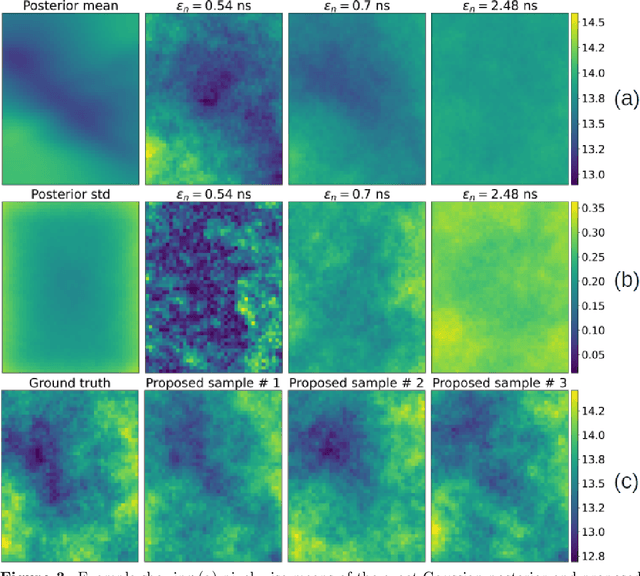
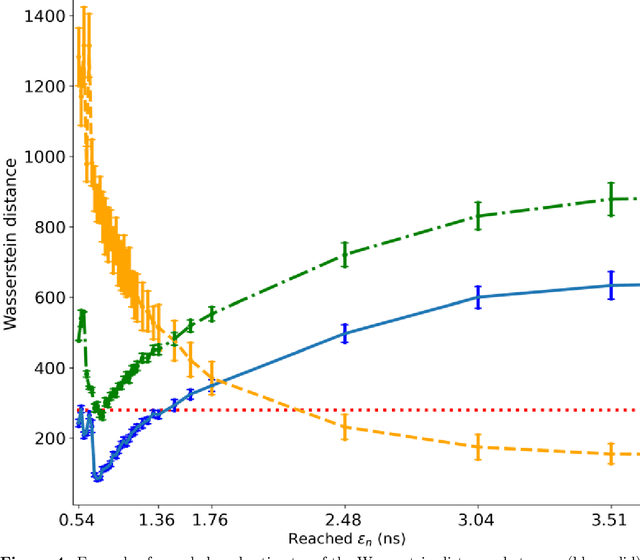
We propose a novel approach for solving inverse-problems with high-dimensional inputs and an expensive forward mapping. It leverages joint deep generative modelling to transfer the original problem spaces to a lower dimensional latent space. By jointly modelling input and output variables and endowing the latent with a prior distribution, the fitted probabilistic model indirectly gives access to the approximate conditional distributions of interest. Since model error and observational noise with unknown distributions are common in practice, we resort to likelihood-free inference with Approximate Bayesian Computation (ABC). Our method calls on ABC by Subset Simulation to explore the regions of the latent space with dissimilarities between generated and observed outputs below prescribed thresholds. We diagnose the diversity of approximate posterior solutions by monitoring the probability content of these regions as a function of the threshold. We further analyze the curvature of the resulting diagnostic curve to propose an adequate ABC threshold. When applied to a cross-borehole tomography example from geophysics, our approach delivers promising performance without using prior knowledge of the forward nor of the noise distribution.

Inversion using a new low-dimensional representation of complex binary geological media based on a deep neural network

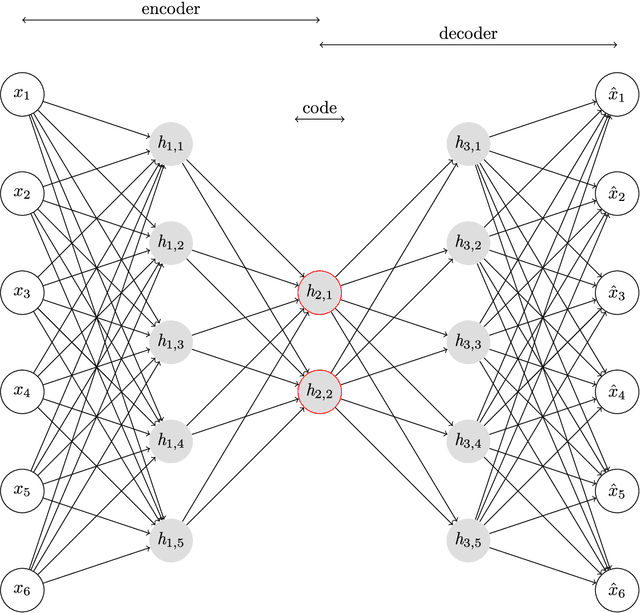
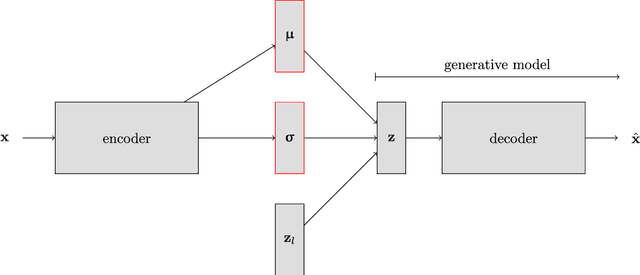
Efficient and high-fidelity prior sampling and inversion for complex geological media is still a largely unsolved challenge. Here, we use a deep neural network of the variational autoencoder type to construct a parametric low-dimensional base model parameterization of complex binary geological media. For inversion purposes, it has the attractive feature that random draws from an uncorrelated standard normal distribution yield model realizations with spatial characteristics that are in agreement with the training set. In comparison with the most commonly used parametric representations in probabilistic inversion, we find that our dimensionality reduction (DR) approach outperforms principle component analysis (PCA), optimization-PCA (OPCA) and discrete cosine transform (DCT) DR techniques for unconditional geostatistical simulation of a channelized prior model. For the considered examples, important compression ratios (200 - 500) are achieved. Given that the construction of our parameterization requires a training set of several tens of thousands of prior model realizations, our DR approach is more suited for probabilistic (or deterministic) inversion than for unconditional (or point-conditioned) geostatistical simulation. Probabilistic inversions of 2D steady-state and 3D transient hydraulic tomography data are used to demonstrate the DR-based inversion. For the 2D case study, the performance is superior compared to current state-of-the-art multiple-point statistics inversion by sequential geostatistical resampling (SGR). Inversion results for the 3D application are also encouraging.

Efficient training-image based geostatistical simulation and inversion using a spatial generative adversarial neural network

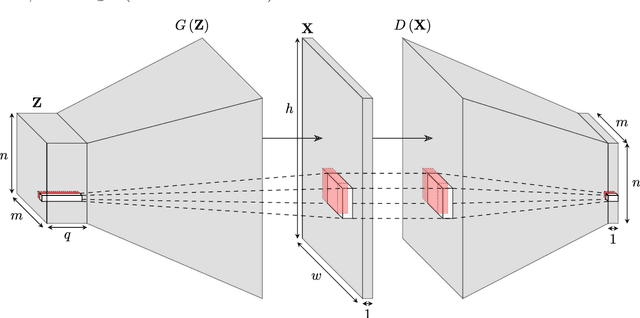
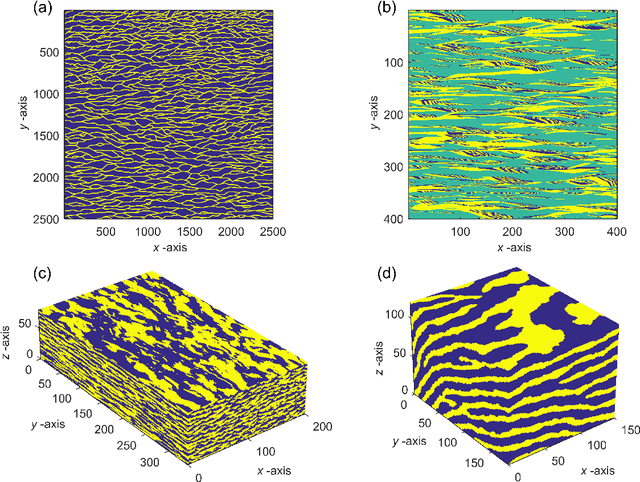
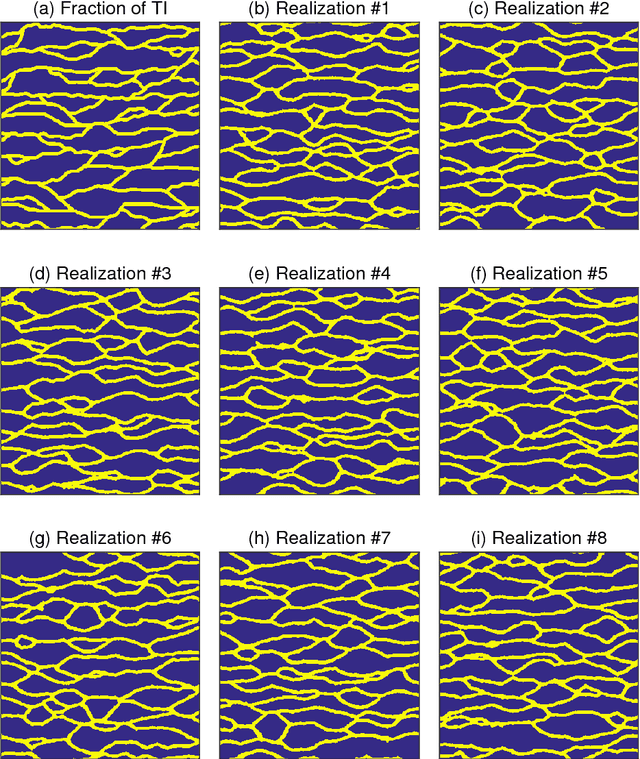
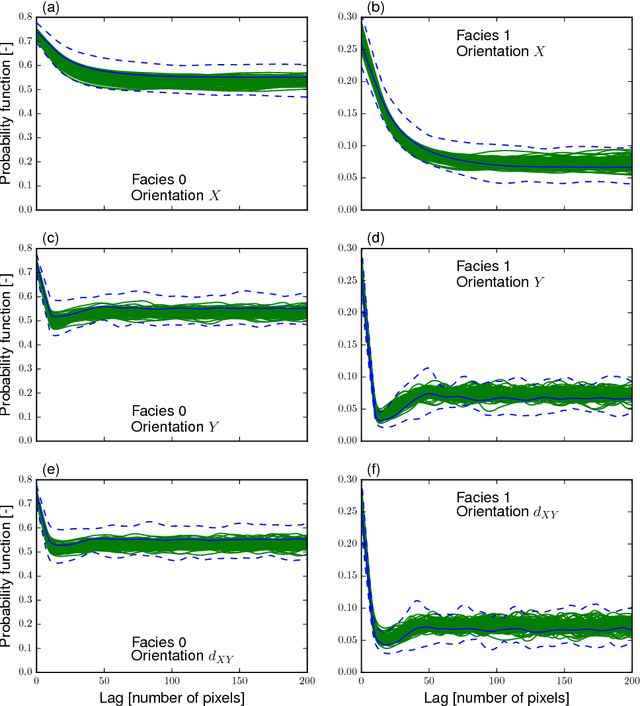
Probabilistic inversion within a multiple-point statistics framework is still computationally prohibitive for large-scale problems. To partly address this, we introduce and evaluate a new training-image based simulation and inversion approach for complex geologic media. Our approach relies on a deep neural network of the spatial generative adversarial network (SGAN) type. After training using a training image (TI), our proposed SGAN can quickly generate 2D and 3D unconditional realizations. A key feature of our SGAN is that it defines a (very) low-dimensional parameterization, thereby allowing for efficient probabilistic (or deterministic) inversion using state-of-the-art Markov chain Monte Carlo (MCMC) methods. A series of 2D and 3D categorical TIs is first used to analyze the performance of our SGAN for unconditional simulation. The speed at which realizations are generated makes it especially useful for simulating over large grids and/or from a complex multi-categorical TI. Subsequently, synthetic inversion case studies involving 2D steady-state flow and 3D transient hydraulic tomography are used to illustrate the effectiveness of our proposed SGAN-based probabilistic inversion. For the 2D case, the inversion rapidly explores the posterior model distribution. For the 3D case, the inversion recovers model realizations that fit the data close to the target level and visually resemble the true model well. Future work will focus on the inclusion of direct conditioning data and application to continuous TIs.