Physics-informed Reduced Order Modeling of Time-dependent PDEs via Differentiable Solvers

Reduced-order modeling (ROM) of time-dependent and parameterized differential equations aims to accelerate the simulation of complex high-dimensional systems by learning a compact latent manifold representation that captures the characteristics of the solution fields and their time-dependent dynamics. Although high-fidelity numerical solvers generate the training datasets, they have thus far been excluded from the training process, causing the learned latent dynamics to drift away from the discretized governing physics. This mismatch often limits generalization and forecasting capabilities. In this work, we propose Physics-informed ROM ($\Phi$-ROM) by incorporating differentiable PDE solvers into the training procedure. Specifically, the latent space dynamics and its dependence on PDE parameters are shaped directly by the governing physics encoded in the solver, ensuring a strong correspondence between the full and reduced systems. Our model outperforms state-of-the-art data-driven ROMs and other physics-informed strategies by accurately generalizing to new dynamics arising from unseen parameters, enabling long-term forecasting beyond the training horizon, maintaining continuity in both time and space, and reducing the data cost. Furthermore, $\Phi$-ROM learns to recover and forecast the solution fields even when trained or evaluated with sparse and irregular observations of the fields, providing a flexible framework for field reconstruction and data assimilation. We demonstrate the framework's robustness across different PDE solvers and highlight its broad applicability by providing an open-source JAX implementation readily extensible to other PDE systems and differentiable solvers.

UV-Net: Learning from Curve-Networks and Solids

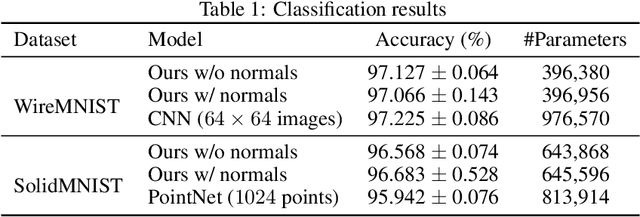
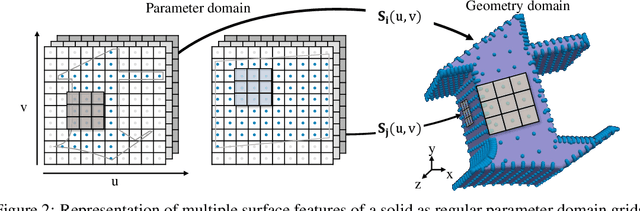
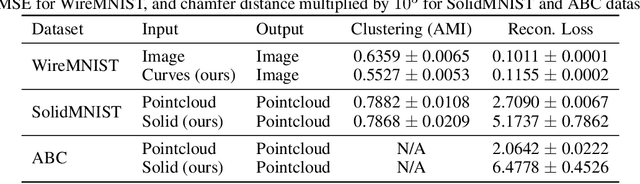
Parametric curves, surfaces and boundary representations are the basis for 2D vector graphics and 3D industrial designs. Despite their prevalence, there exists limited research on applying modern deep neural networks directly to such representations. The unique challenges in working with such representations arise from the combination of continuous non-Euclidean geometry domain and discrete topology, as well as a lack of labeled datasets, benchmarks and baseline models. In this paper, we propose a unified representation for parametric curve-networks and solids by exploiting the u- and uv-parameter domains of curve and surfaces, respectively, to model the geometry, and an adjacency graph to explicitly model the topology. This leads to a unique and efficient network architecture based on coupled image and graph convolutional neural networks to extract features from curve-networks and solids. Inspired by the MNIST image dataset, we create and publish WireMNIST (for 2D curve-networks) and SolidMNIST (for 3D solids), two related labeled datasets depicting alphabets to encourage future research in this area. We demonstrate the effectiveness of our method using supervised and self-supervised tasks on our new datasets, as well as the publicly available ABC dataset. The results demonstrate the effectiveness of our representation and provide a competitive baseline for learning tasks involving curve-networks and solids.