Nick Gravin
Testing Symmetric Markov Chains from a Single Trajectory
Dec 04, 2017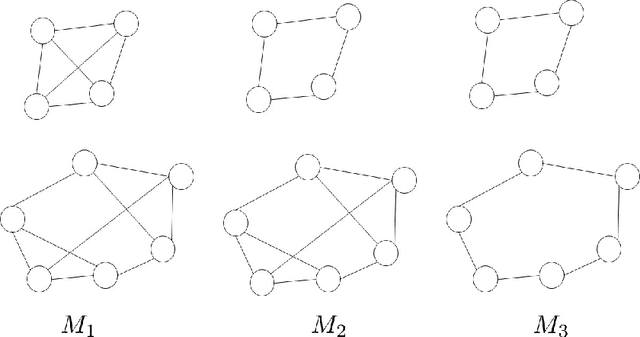

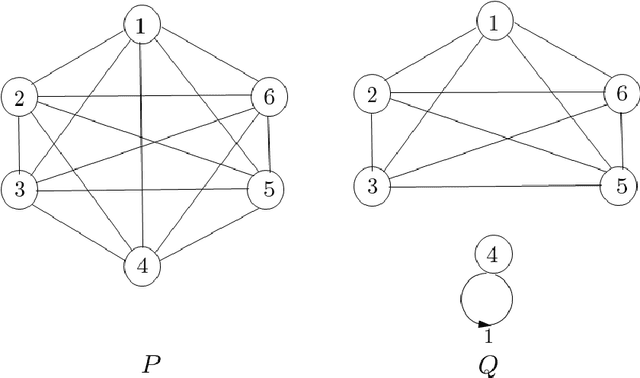
Abstract:Classical distribution testing assumes access to i.i.d. samples from the distribution that is being tested. We initiate the study of Markov chain testing, assuming access to a single trajectory of a Markov Chain. In particular, we observe a single trajectory X0,...,Xt,... of an unknown, symmetric, and finite state Markov Chain M. We do not control the starting state X0, and we cannot restart the chain. Given our single trajectory, the goal is to test whether M is identical to a model Markov Chain M0 , or far from it under an appropriate notion of difference. We propose a measure of difference between two Markov chains, motivated by the early work of Kazakos [Kaz78], which captures the scaling behavior of the total variation distance between trajectories sampled from the Markov chains as the length of these trajectories grows. We provide efficient testers and information-theoretic lower bounds for testing identity of symmetric Markov chains under our proposed measure of difference, which are tight up to logarithmic factors if the hitting times of the model chain M0 is O(n) in the size of the state space n.
Tight Lower Bounds for Multiplicative Weights Algorithmic Families
Jul 14, 2016
Abstract:We study the fundamental problem of prediction with expert advice and develop regret lower bounds for a large family of algorithms for this problem. We develop simple adversarial primitives, that lend themselves to various combinations leading to sharp lower bounds for many algorithmic families. We use these primitives to show that the classic Multiplicative Weights Algorithm (MWA) has a regret of $\sqrt{\frac{T \ln k}{2}}$, there by completely closing the gap between upper and lower bounds. We further show a regret lower bound of $\frac{2}{3}\sqrt{\frac{T\ln k}{2}}$ for a much more general family of algorithms than MWA, where the learning rate can be arbitrarily varied over time, or even picked from arbitrary distributions over time. We also use our primitives to construct adversaries in the geometric horizon setting for MWA to precisely characterize the regret at $\frac{0.391}{\sqrt{\delta}}$ for the case of $2$ experts and a lower bound of $\frac{1}{2}\sqrt{\frac{\ln k}{2\delta}}$ for the case of arbitrary number of experts $k$.
Towards Optimal Algorithms for Prediction with Expert Advice
Jul 11, 2016Abstract:We study the classical problem of prediction with expert advice in the adversarial setting with a geometric stopping time. In 1965, Cover gave the optimal algorithm for the case of 2 experts. In this paper, we design the optimal algorithm, adversary and regret for the case of 3 experts. Further, we show that the optimal algorithm for $2$ and $3$ experts is a probability matching algorithm (analogous to Thompson sampling) against a particular randomized adversary. Remarkably, our proof shows that the probability matching algorithm is not only optimal against this particular randomized adversary, but also minimax optimal. Our analysis develops upper and lower bounds simultaneously, analogous to the primal-dual method. Our analysis of the optimal adversary goes through delicate asymptotics of the random walk of a particle between multiple walls. We use the connection we develop to random walks to derive an improved algorithm and regret bound for the case of $4$ experts, and, provide a general framework for designing the optimal algorithm and adversary for an arbitrary number of experts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge