Utilizing the Structure of the Curvelet Transform with Compressed Sensing

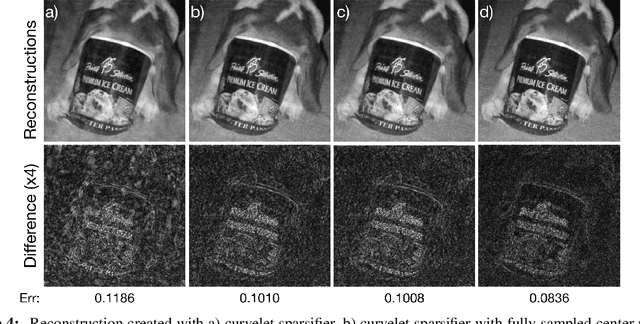
The discrete curvelet transform decomposes an image into a set of fundamental components that are distinguished by direction and size as well as a low-frequency representation. The curvelet representation is approximately sparse; thus, it is a useful sparsifying transformation to be used with compressed sensing. Although the curvelet transform of a natural image is sparse, the low-frequency portion is not. This manuscript presents a method to modify the sparsifying transformation to take advantage of this fact. Instead of relying on sparsity for this low-frequency estimate, the Nyquist-Shannon theorem specifies a square region to be collected centered on the $0$ frequency. A Basis Pursuit Denoising problem is solved to determine the missing details after modifying the sparisfying transformation to take advantage of the known fully sampled region. Finally, by taking advantage of this structure with a redundant dictionary comprised of both the wavelet and curvelet transforms, additional gains in quality are achieved.