Agent Environment Cycle Games

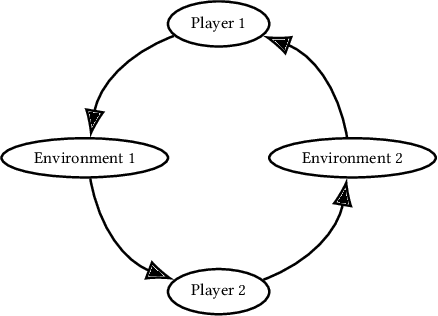
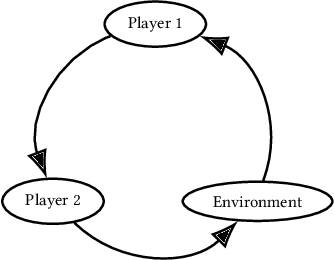
Partially Observable Stochastic Games (POSGs), are the most general model of games used in Multi-Agent Reinforcement Learning (MARL), modeling actions and observations as happening sequentially for all agents. We introduce Agent Environment Cycle Games (AEC Games), a model of games based on sequential agent actions and observations. AEC Games can be thought of as sequential versions of POSGs, and we prove that they are equally powerful. We argue conceptually and through case studies that the AEC games model is useful in important scenarios in MARL for which the POSG model is not well suited. We additionally introduce "cyclically expansive curriculum learning," a new MARL curriculum learning method motivated by the AEC games model. It can be applied "for free," and experimentally we show this technique to achieve up to 35.1% more total reward on average.

Multi-Agent Informational Learning Processes

We introduce a new mathematical model of multi-agent reinforcement learning,the Multi-Agent Informational Learning Process or "MAILP" model. The model is based on the notion that agents have policies for a certain amount of information, models how this information iteratively evolves and propagates through manyagents. This model is very general, and the only meaningful assumption made is that learning for individual agents progressively slows over time.

Parameter Sharing is Surprisingly Useful for Multi-Agent Deep Reinforcement Learning

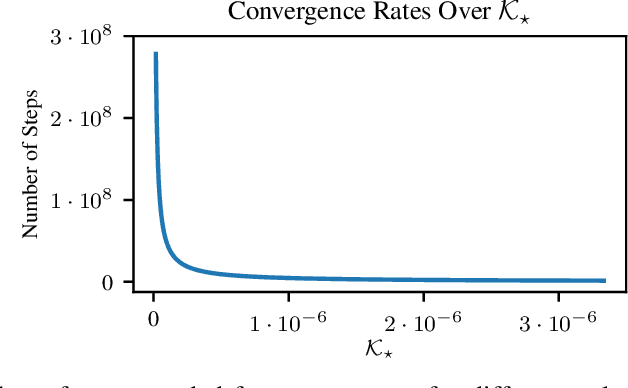
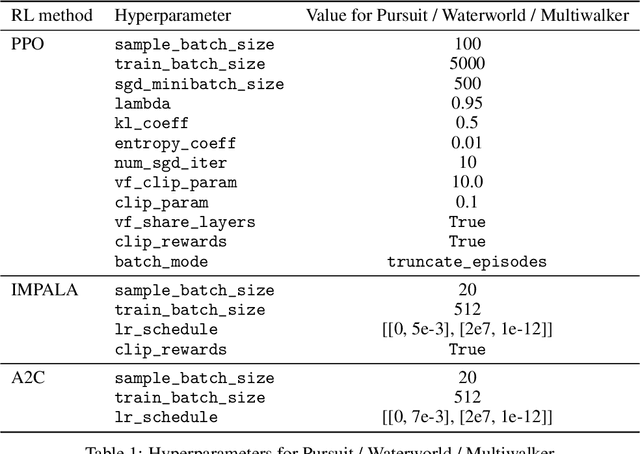
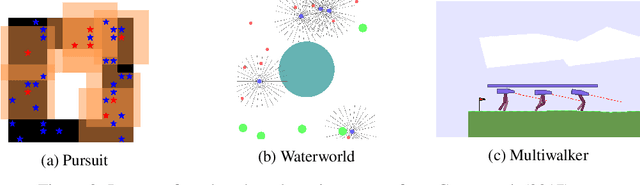
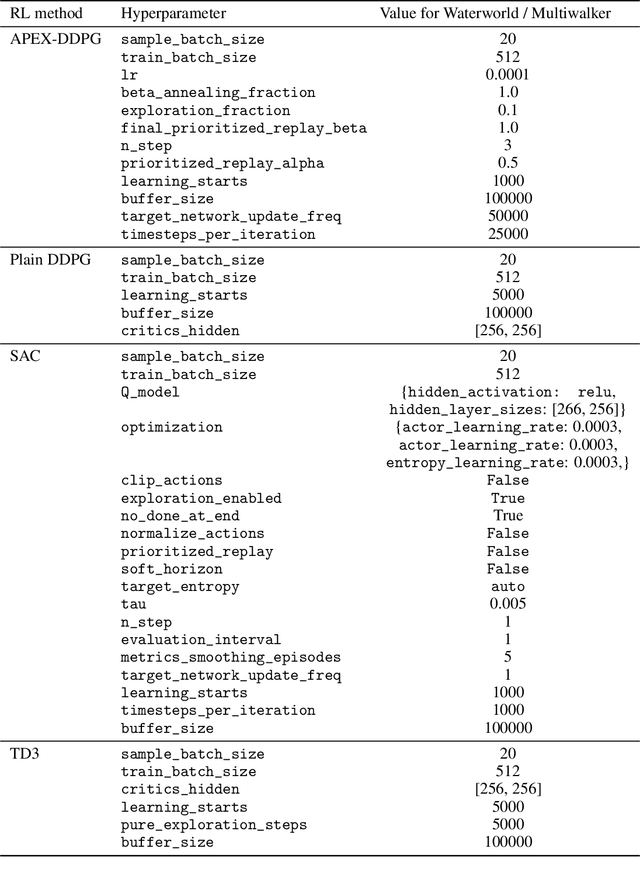
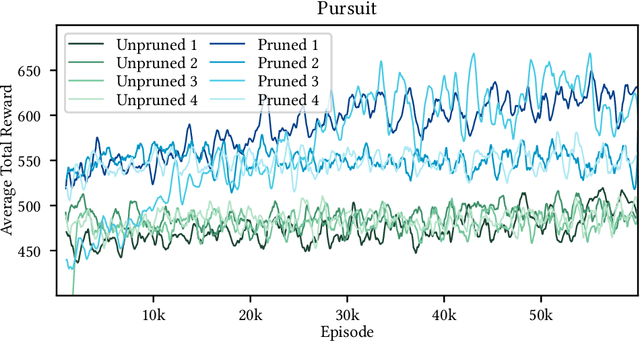
"Nonstationarity" is a fundamental problem in cooperative multi-agent reinforcement learning (MARL)--each agent must relearn information about the other agent's policies due to the other agents learning, causing information to "ring" between agents and convergence to be slow. The MAILP model, introduced by Terry and Grammel (2020), is a novel model of information transfer during multi-agent learning. We use the MAILP model to show that increasing training centralization arbitrarily mitigates the slowing of convergence due to nonstationarity. The most centralized case of learning is parameter sharing, an uncommonly used MARL method, specific to environments with homogeneous agents, that bootstraps a single-agent reinforcement learning (RL) method and learns an identical policy for each agent. We experimentally replicate the result of increased learning centralization leading to better performance on the MARL benchmark set from Gupta et al. (2017). We further apply parameter sharing to 8 "more modern" single-agent deep RL (DRL) methods for the first time in the literature. With this, we achieved the best documented performance on a set of MARL benchmarks and achieved up to 38 times more average reward in as little as 7% as many episodes compared to documented parameter sharing arrangement. We finally offer a formal proof of a set of methods that allow parameter sharing to serve in environments with heterogeneous agents.

Scenario Submodular Cover

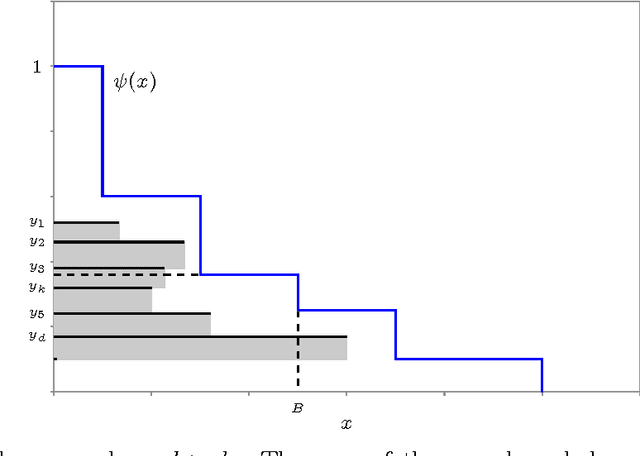
Many problems in Machine Learning can be modeled as submodular optimization problems. Recent work has focused on stochastic or adaptive versions of these problems. We consider the Scenario Submodular Cover problem, which is a counterpart to the Stochastic Submodular Cover problem studied by Golovin and Krause. In Scenario Submodular Cover, the goal is to produce a cover with minimum expected cost, where the expectation is with respect to an empirical joint distribution, given as input by a weighted sample of realizations. In contrast, in Stochastic Submodular Cover, the variables of the input distribution are assumed to be independent, and the distribution of each variable is given as input. Building on algorithms developed by Cicalese et al. and Golovin and Krause for related problems, we give two approximation algorithms for Scenario Submodular Cover over discrete distributions. The first achieves an approximation factor of O(log Qm), where m is the size of the sample and Q is the goal utility. The second, simpler algorithm achieves an approximation bound of O(log QW), where Q is the goal utility and W is the sum of the integer weights. (Both bounds assume an integer-valued utility function.) Our results yield approximation bounds for other problems involving non-independent distributions that are explicitly specified by their support.