Ranked differences Pearson correlation dissimilarity with an application to electricity users time series clustering

Time series clustering is an unsupervised learning method for classifying time series data into groups with similar behavior. It is used in applications such as healthcare, finance, economics, energy, and climate science. Several time series clustering methods have been introduced and used for over four decades. Most of them focus on measuring either Euclidean distances or association dissimilarities between time series. In this work, we propose a new dissimilarity measure called ranked Pearson correlation dissimilarity (RDPC), which combines a weighted average of a specified fraction of the largest element-wise differences with the well-known Pearson correlation dissimilarity. It is incorporated into hierarchical clustering. The performance is evaluated and compared with existing clustering algorithms. The results show that the RDPC algorithm outperforms others in complicated cases involving different seasonal patterns, trends, and peaks. Finally, we demonstrate our method by clustering a random sample of customers from a Thai electricity consumption time series dataset into seven groups with unique characteristics.

A Bayesian cluster validity index

Selecting the appropriate number of clusters is a critical step in applying clustering algorithms. To assist in this process, various cluster validity indices (CVIs) have been developed. These indices are designed to identify the optimal number of clusters within a dataset. However, users may not always seek the absolute optimal number of clusters but rather a secondary option that better aligns with their specific applications. This realization has led us to introduce a Bayesian cluster validity index (BCVI), which builds upon existing indices. The BCVI utilizes either Dirichlet or generalized Dirichlet priors, resulting in the same posterior distribution. We evaluate our BCVI using the Wiroonsri index for hard clustering and the Wiroonsri-Preedasawakul index for soft clustering as underlying indices. We compare the performance of our proposed BCVI with that of the original underlying indices and several other existing CVIs, including Davies-Bouldin, Starczewski, Xie-Beni, and KWON2 indices. Our BCVI offers clear advantages in situations where user expertise is valuable, allowing users to specify their desired range for the final number of clusters. To illustrate this, we conduct experiments classified into three different scenarios. Additionally, we showcase the practical applicability of our approach through real-world datasets, such as MRI brain tumor images. These tools will be published as a new R package 'BayesCVI'.

A correlation-based fuzzy cluster validity index with secondary options detector

The optimal number of clusters is one of the main concerns when applying cluster analysis. Several cluster validity indexes have been introduced to address this problem. However, in some situations, there is more than one option that can be chosen as the final number of clusters. This aspect has been overlooked by most of the existing works in this area. In this study, we introduce a correlation-based fuzzy cluster validity index known as the Wiroonsri-Preedasawakul (WP) index. This index is defined based on the correlation between the actual distance between a pair of data points and the distance between adjusted centroids with respect to that pair. We evaluate and compare the performance of our index with several existing indexes, including Xie-Beni, Pakhira-Bandyopadhyay-Maulik, Tang, Wu-Li, generalized C, and Kwon2. We conduct this evaluation on four types of datasets: artificial datasets, real-world datasets, simulated datasets with ranks, and image datasets, using the fuzzy c-means algorithm. Overall, the WP index outperforms most, if not all, of these indexes in terms of accurately detecting the optimal number of clusters and providing accurate secondary options. Moreover, our index remains effective even when the fuzziness parameter $m$ is set to a large value. Our R package called WPfuzzyCVIs used in this work is also available in https://github.com/nwiroonsri/WPfuzzyCVIs.

Clustering performance analysis using new correlation based cluster validity indices

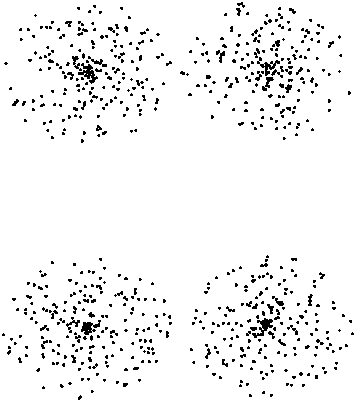
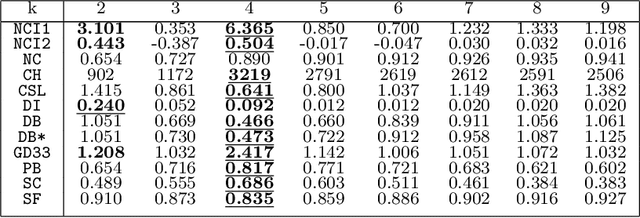
There are various cluster validity measures used for evaluating clustering results. One of the main objective of using these measures is to seek the optimal unknown number of clusters. Some measures work well for clusters with different densities, sizes and shapes. Yet, one of the weakness that those validity measures share is that they sometimes provide only one clear optimal number of clusters. That number is actually unknown and there might be more than one potential sub-optimal options that a user may wish to choose based on different applications. We develop two new cluster validity indices based on a correlation between an actual distance between a pair of data points and a centroid distance of clusters that the two points locate in. Our proposed indices constantly yield several peaks at different numbers of clusters which overcome the weakness previously stated. Furthermore, the introduced correlation can also be used for evaluating the quality of a selected clustering result. Several experiments in different scenarios including the well-known iris data set and a real-world marketing application have been conducted in order to compare the proposed validity indices with several well-known ones.