K-VARK: Kernelized Variance-Aware Residual Kalman Filter for Sensorless Force Estimation in Collaborative Robots

Reliable estimation of contact forces is crucial for ensuring safe and precise interaction of robots with unstructured environments. However, accurate sensorless force estimation remains challenging due to inherent modeling errors and complex residual dynamics and friction. To address this challenge, in this paper, we propose K-VARK (Kernelized Variance-Aware Residual Kalman filter), a novel approach that integrates a kernelized, probabilistic model of joint residual torques into an adaptive Kalman filter framework. Through Kernelized Movement Primitives trained on optimized excitation trajectories, K-VARK captures both the predictive mean and input-dependent heteroscedastic variance of residual torques, reflecting data variability and distance-to-training effects. These statistics inform a variance-aware virtual measurement update by augmenting the measurement noise covariance, while the process noise covariance adapts online via variational Bayesian optimization to handle dynamic disturbances. Experimental validation on a 6-DoF collaborative manipulator demonstrates that K-VARK achieves over 20% reduction in RMSE compared to state-of-the-art sensorless force estimation methods, yielding robust and accurate external force/torque estimation suitable for advanced tasks such as polishing and assembly.

Geometric Reinforcement Learning: The Case of Cartesian Space Orientation

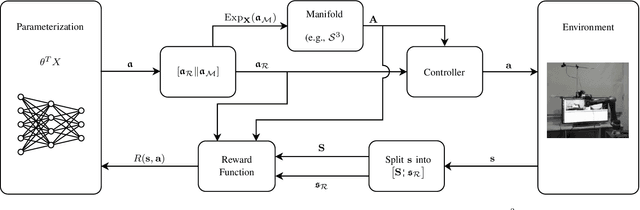
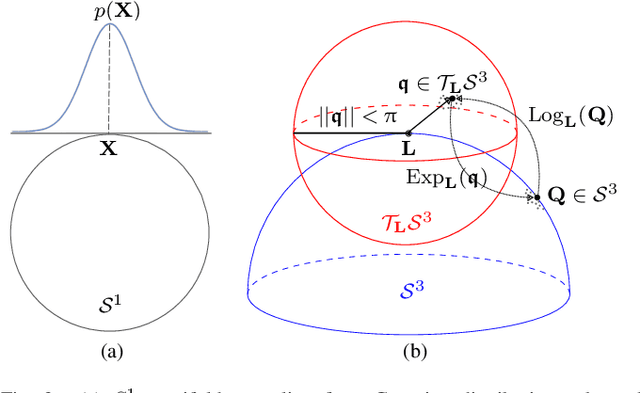
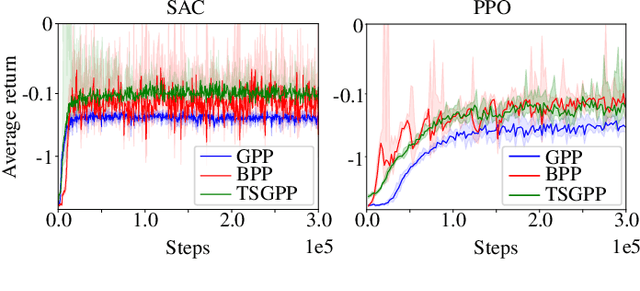
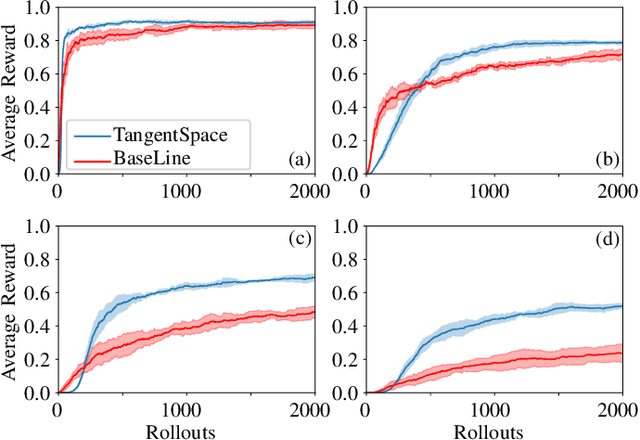
Reinforcement learning (RL) enables an agent to learn by trial and error while interacting with a dynamic environment. Traditionally, RL is used to learn and predict Euclidean robotic manipulation skills like positions, velocities, and forces. However, in robotics, it is common to have non-Euclidean data like orientation or stiffness, and neglecting their geometric nature can adversely affect learning performance and accuracy. In this paper, we propose a novel framework for RL by using Riemannian geometry, and show how it can be applied to learn manipulation skills with a specific geometric structure (e.g., robot's orientation in the task space). The proposed framework is suitable for any policy representation and is independent of the algorithm choice. Specifically, we propose to apply policy parameterization and learning on the tangent space, then map the learned actions back to the appropriate manifold (e.g., the S3 manifold for orientation). Therefore, we introduce a geometrically grounded pre- and post-processing step into the typical RL pipeline, which opens the door to all algorithms designed for Euclidean space to learn from non-Euclidean data without changes. Experimental results, obtained both in simulation and on a real robot, support our hypothesis that learning on the tangent space is more accurate and converges to a better solution than approximating non-Euclidean data.