Sparse Offline Reinforcement Learning with Corruption Robustness

We investigate robustness to strong data corruption in offline sparse reinforcement learning (RL). In our setting, an adversary may arbitrarily perturb a fraction of the collected trajectories from a high-dimensional but sparse Markov decision process, and our goal is to estimate a near optimal policy. The main challenge is that, in the high-dimensional regime where the number of samples $N$ is smaller than the feature dimension $d$, exploiting sparsity is essential for obtaining non-vacuous guarantees but has not been systematically studied in offline RL. We analyse the problem under uniform coverage and sparse single-concentrability assumptions. While Least Square Value Iteration (LSVI), a standard approach for robust offline RL, performs well under uniform coverage, we show that integrating sparsity into LSVI is unnatural, and its analysis may break down due to overly pessimistic bonuses. To overcome this, we propose actor-critic methods with sparse robust estimator oracles, which avoid the use of pointwise pessimistic bonuses and provide the first non-vacuous guarantees for sparse offline RL under single-policy concentrability coverage. Moreover, we extend our results to the contaminated setting and show that our algorithm remains robust under strong contamination. Our results provide the first non-vacuous guarantees in high-dimensional sparse MDPs with single-policy concentrability coverage and corruption, showing that learning a near-optimal policy remains possible in regimes where traditional robust offline RL techniques may fail.

Near-optimal Reconfigurable Intelligent Surface Configuration: Blind Beamforming with Sensing

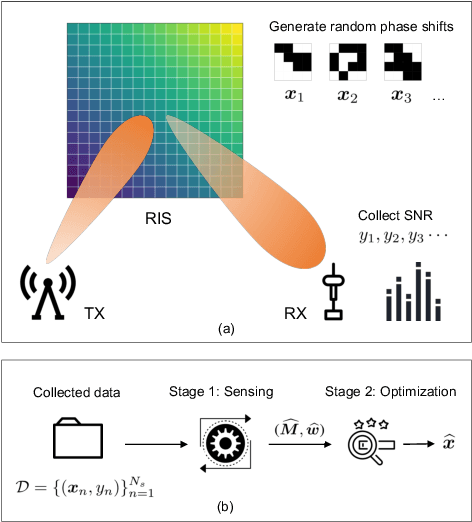
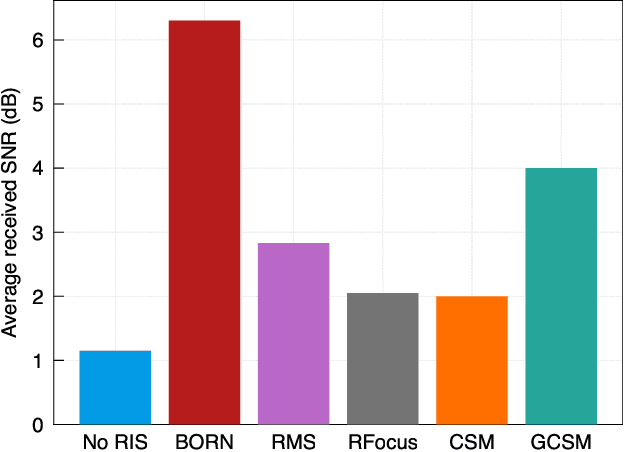
Blind beamforming has emerged as a promising approach to configure reconfigurable intelligent surfaces (RISs) without relying on channel state information (CSI) or geometric models, making it directly compatible with commodity hardware. In this paper, we propose a new blind beamforming algorithm, so-called Blind Optimal RIS Beamforming with Sensing (\textsc{BORN}), that operates using only received signal strength (RSS). In contrast to existing methods that rely on majority-voting mechanisms, \textsc{BORN} exploits the intrinsic quadratic structure of the received signal-to-noise ratio (SNR). The algorithm proceeds in two stages: \emph{sensing}, where a quadratic model is estimated from RSS measurements, and \emph{optimization}, where the RIS configuration is obtained using the estimated quadratic model. Our novelties are twofold. Firstly, we show for the first time, that \textsc{BORN} can achieve provable near-optimal performance using only $O(N \log_2(N))$ samples, where $N$ is the number of RIS elements. As a by-product of our analysis, we show that quadratic models are learnable under Rademacher feature distributions when the second-order coefficient matrix is low-rank. This result, to our knowledge, has not been established in prior matrix sensing literature. Secondly, extensive simulations and real-world field tests demonstrate that \textsc{BORN} achieves near-optimal performance, substantially outperforming state-of-the-art blind beamforming algorithms, particularly in scenarios with a weak background channel such as non-line-of-sight (NLOS).

Symmetric Linear Bandits with Hidden Symmetry

High-dimensional linear bandits with low-dimensional structure have received considerable attention in recent studies due to their practical significance. The most common structure in the literature is sparsity. However, it may not be available in practice. Symmetry, where the reward is invariant under certain groups of transformations on the set of arms, is another important inductive bias in the high-dimensional case that covers many standard structures, including sparsity. In this work, we study high-dimensional symmetric linear bandits where the symmetry is hidden from the learner, and the correct symmetry needs to be learned in an online setting. We examine the structure of a collection of hidden symmetry and provide a method based on model selection within the collection of low-dimensional subspaces. Our algorithm achieves a regret bound of $ O(d_0^{1/3} T^{2/3} \log(d))$, where $d$ is the ambient dimension which is potentially very large, and $d_0$ is the dimension of the true low-dimensional subspace such that $d_0 \ll d$. With an extra assumption on well-separated models, we can further improve the regret to $ O(d_0\sqrt{T\log(d)} )$.

Learning the Expected Core of Strictly Convex Stochastic Cooperative Games

Reward allocation, also known as the credit assignment problem, has been an important topic in economics, engineering, and machine learning. An important concept in credit assignment is the core, which is the set of stable allocations where no agent has the motivation to deviate from the grand coalition. In this paper, we consider the stable allocation learning problem of stochastic cooperative games, where the reward function is characterised as a random variable with an unknown distribution. Given an oracle that returns a stochastic reward for an enquired coalition each round, our goal is to learn the expected core, that is, the set of allocations that are stable in expectation. Within the class of strictly convex games, we present an algorithm named \texttt{Common-Points-Picking} that returns a stable allocation given a polynomial number of samples, with high probability. The analysis of our algorithm involves the development of several new results in convex geometry, including an extension of the separation hyperplane theorem for multiple convex sets, and may be of independent interest.

Invariant Lipschitz Bandits: A Side Observation Approach

Symmetry arises in many optimization and decision-making problems, and has attracted considerable attention from the optimization community: By utilizing the existence of such symmetries, the process of searching for optimal solutions can be improved significantly. Despite its success in (offline) optimization, the utilization of symmetries has not been well examined within the online optimization settings, especially in the bandit literature. As such, in this paper we study the invariant Lipschitz bandit setting, a subclass of the Lipschitz bandits where the reward function and the set of arms are preserved under a group of transformations. We introduce an algorithm named \texttt{UniformMesh-N}, which naturally integrates side observations using group orbits into the \texttt{UniformMesh} algorithm (\cite{Kleinberg2005_UniformMesh}), which uniformly discretizes the set of arms. Using the side-observation approach, we prove an improved regret upper bound, which depends on the cardinality of the group, given that the group is finite. We also prove a matching regret's lower bound for the invariant Lipschitz bandit class (up to logarithmic factors). We hope that our work will ignite further investigation of symmetry in bandit theory and sequential decision-making theory in general.