Cryptographic transformations over polyadic rings

This article introduces a novel cryptographic paradigm based on nonderived polyadic algebraic structures. Traditional cryptosystems rely on binary operations within groups, rings, or fields, whose well-understood properties can be exploited in cryptanalysis. To overcome these vulnerabilities, we propose a shift to polyadic rings, which generalize classical rings by allowing operations of higher arity: an $m$-ary addition and an $n$-ary multiplication. The foundation of our approach is the construction of polyadic integers -- congruence classes of ordinary integers endowed with such $m$-ary and $n$-ary operations. A key innovation is the parameter-to-arity mapping $Φ(a,b)=(m,n)$, which links the parameters $(a,b)$ defining a congruence class to the specific arities required for algebraic closure. This mapping is mathematically intricate: it is non-injective, non-surjective, and multivalued. This complex, non-unique relationship forms the core of the proposed cryptosystem's security. We present two concrete encryption procedures that leverage this structure by encoding plaintext within the parameters of polyadic rings and transmitting information via polyadically quantized analog signals. In one method, plaintext is linked to the additive arity $m_{i}$ and secured using the summation of such signals; in the other, it is linked to a ring parameter $a_{i}$ and secured using their multiplication. In both cases, the "quantized" nature of polyadic operations generates systems of equations that are straightforward for a legitimate recipient with the correct key but exceptionally difficult for an attacker without it. The resulting framework promises a substantial increase in cryptographic security. This work establishes the theoretical foundation for this new class of encryption schemes and highlights their potential for constructing robust, next-generation cryptographic protocols.

Robust Local Search for Solving RCPSP/max with Durational Uncertainty

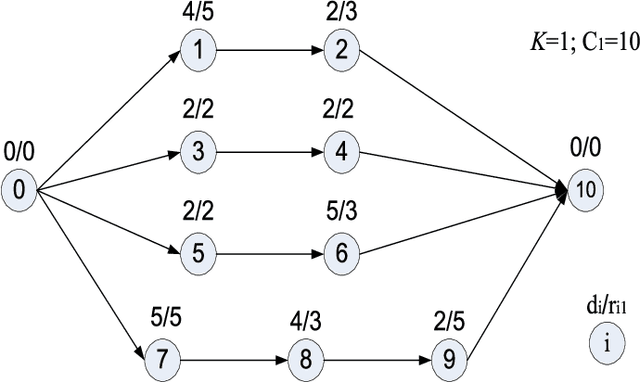
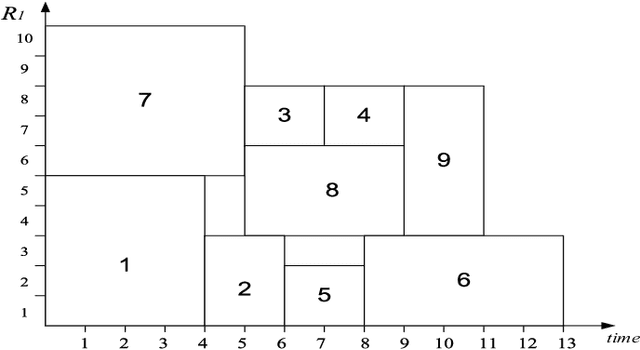
Scheduling problems in manufacturing, logistics and project management have frequently been modeled using the framework of Resource Constrained Project Scheduling Problems with minimum and maximum time lags (RCPSP/max). Due to the importance of these problems, providing scalable solution schedules for RCPSP/max problems is a topic of extensive research. However, all existing methods for solving RCPSP/max assume that durations of activities are known with certainty, an assumption that does not hold in real world scheduling problems where unexpected external events such as manpower availability, weather changes, etc. lead to delays or advances in completion of activities. Thus, in this paper, our focus is on providing a scalable method for solving RCPSP/max problems with durational uncertainty. To that end, we introduce the robust local search method consisting of three key ideas: (a) Introducing and studying the properties of two decision rule approximations used to compute start times of activities with respect to dynamic realizations of the durational uncertainty; (b) Deriving the expression for robust makespan of an execution strategy based on decision rule approximations; and (c) A robust local search mechanism to efficiently compute activity execution strategies that are robust against durational uncertainty. Furthermore, we also provide enhancements to local search that exploit temporal dependencies between activities. Our experimental results illustrate that robust local search is able to provide robust execution strategies efficiently.