Infinite-Dimensional Operator/Block Kaczmarz Algorithms: Regret Bounds and $λ$-Effectiveness

We present a variety of projection-based linear regression algorithms with a focus on modern machine-learning models and their algorithmic performance. We study the role of the relaxation parameter in generalized Kaczmarz algorithms and establish a priori regret bounds with explicit $λ$-dependence to quantify how much an algorithm's performance deviates from its optimal performance. A detailed analysis of relaxation parameter is also provided. Applications include: explicit regret bounds for the framework of Kaczmarz algorithm models, non-orthogonal Fourier expansions, and the use of regret estimates in modern machine learning models, including for noisy data, i.e., regret bounds for the noisy Kaczmarz algorithms. Motivated by machine-learning practice, our wider framework treats bounded operators (on infinite-dimensional Hilbert spaces), with updates realized as (block) Kaczmarz algorithms, leading to new and versatile results.

Conditional mean embeddings and optimal feature selection via positive definite kernels

Motivated by applications, we consider here new operator theoretic approaches to Conditional mean embeddings (CME). Our present results combine a spectral analysis-based optimization scheme with the use of kernels, stochastic processes, and constructive learning algorithms. For initially given non-linear data, we consider optimization-based feature selections. This entails the use of convex sets of positive definite (p.d.) kernels in a construction of optimal feature selection via regression algorithms from learning models. Thus, with initial inputs of training data (for a suitable learning algorithm,) each choice of p.d. kernel $K$ in turn yields a variety of Hilbert spaces and realizations of features. A novel idea here is that we shall allow an optimization over selected sets of kernels $K$ from a convex set $C$ of positive definite kernels $K$. Hence our \textquotedblleft optimal\textquotedblright{} choices of feature representations will depend on a secondary optimization over p.d. kernels $K$ within a specified convex set $C$.

Operator theory, kernels, and Feedforward Neural Networks

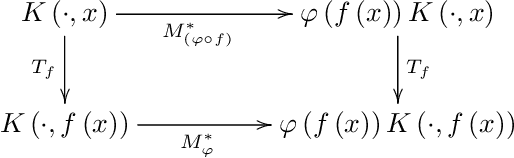
In this paper we show how specific families of positive definite kernels serve as powerful tools in analyses of iteration algorithms for multiple layer feedforward Neural Network models. Our focus is on particular kernels that adapt well to learning algorithms for data-sets/features which display intrinsic self-similarities at feedforward iterations of scaling.