On the application of the Wasserstein metric to 2D curves classification

In this work we analyse a number of variants of the Wasserstein distance which allow to focus the classification on the prescribed parts (fragments) of classified 2D curves. These variants are based on the use of a number of discrete probability measures which reflect the importance of given fragments of curves. The performance of this approach is tested through a series of experiments related to the clustering analysis of 2D curves performed on data coming from the field of archaeology.

A comprehensive study of clustering a class of 2D shapes

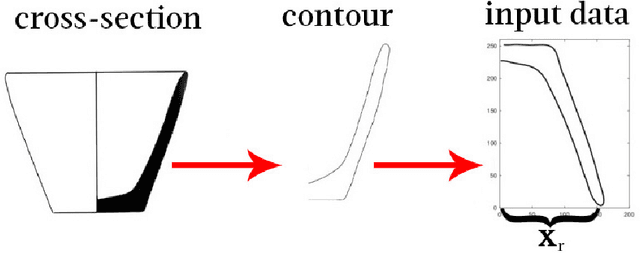
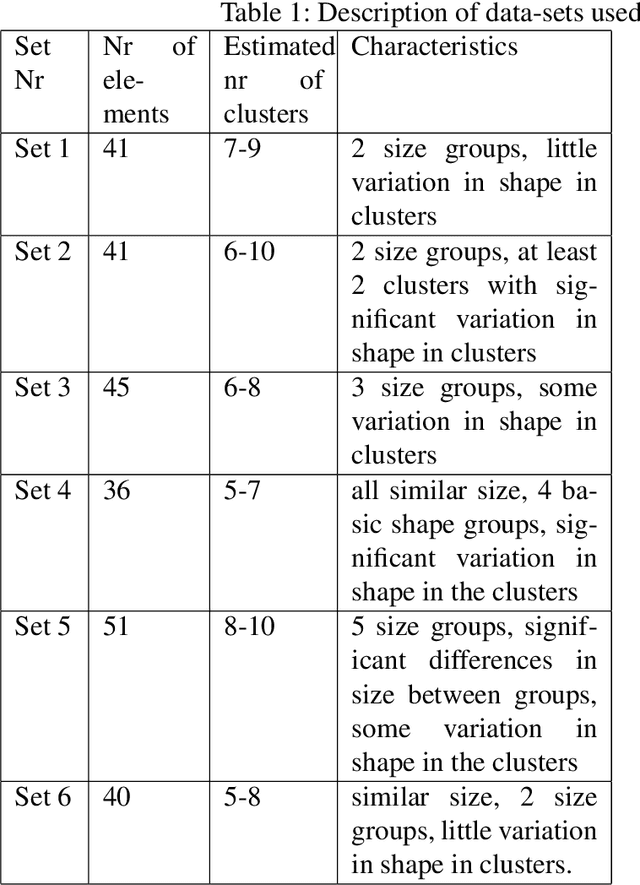
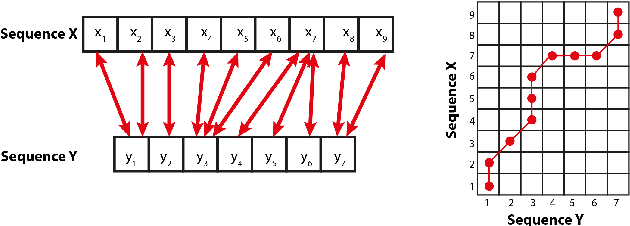
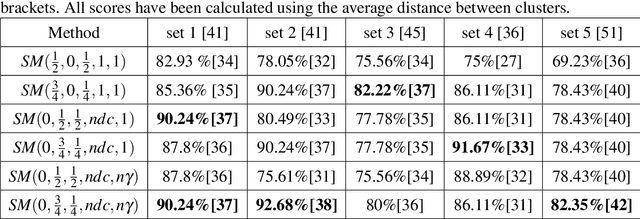
The paper concerns clustering with respect to the shape and size of 2D contours that are boundaries of cross-sections of 3D objects of revolution. We propose a number of similarity measures based on combined disparate Procrustes analysis (PA) and Dynamic Time Warping (DTW) distances. Motivation and the main application for this study comes from archaeology. The performed computational experiments refer to the clustering of archaeological pottery.