Diffusion Model-Based Posterior Sampling in Full Waveform Inversion

Bayesian full waveform inversion (FWI) offers uncertainty-aware subsurface models; however, posterior sampling directly on observed seismic shot records is rarely practical at the field scale because each sample requires numerous wave-equation solves. We aim to make such sampling feasible for large surveys while preserving calibration, that is, high uncertainty in less illuminated areas. Our approach couples diffusion-based posterior sampling with simultaneous-source FWI data. At each diffusion noise level, a network predicts a clean velocity model. We then apply a stochastic refinement step in model space using Langevin dynamics under the wave-equation likelihood and reintroduce noise to decouple successive levels before proceeding. Simultaneous-source batches reduce forward and adjoint solves approximately in proportion to the supergather size, while an unconditional diffusion prior trained on velocity patches and volumes helps suppress source-related numerical artefacts. We evaluate the method on three 2D synthetic datasets (SEG/EAGE Overthrust, SEG/EAGE Salt, SEAM Arid), a 2D field line, and a 3D upscaling study. Relative to a particle-based variational baseline, namely Stein variational gradient descent without a learned prior and with single-source (non-simultaneous-source) FWI, our sampler achieves lower model error and better data fit at a substantially reduced computational cost. By aligning encoded-shot likelihoods with diffusion-based sampling and exploiting straightforward parallelization over samples and source batches, the method provides a practical path to calibrated posterior inference on observed shot records that scales to large 2D and 3D problems.

LatentPINNs: Generative physics-informed neural networks via a latent representation learning

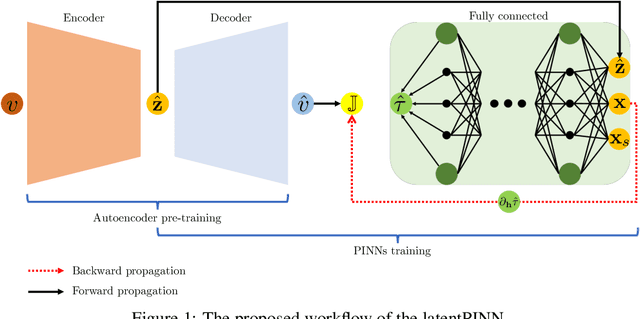
Physics-informed neural networks (PINNs) are promising to replace conventional partial differential equation (PDE) solvers by offering more accurate and flexible PDE solutions. However, they are hampered by the relatively slow convergence and the need to perform additional, potentially expensive, training for different PDE parameters. To solve this limitation, we introduce latentPINN, a framework that utilizes latent representations of the PDE parameters as additional (to the coordinates) inputs into PINNs and allows for training over the distribution of these parameters. Motivated by the recent progress on generative models, we promote the use of latent diffusion models to learn compressed latent representations of the PDE parameters distribution and act as input parameters to NN functional solutions. We use a two-stage training scheme in which the first stage, we learn the latent representations for the distribution of PDE parameters. In the second stage, we train a physics-informed neural network over inputs given by randomly drawn samples from the coordinate space within the solution domain and samples from the learned latent representation of the PDE parameters. We test the approach on a class of level set equations given by the nonlinear Eikonal equation. We specifically share results corresponding to three different sets of Eikonal parameters (velocity models). The proposed method performs well on new phase velocity models without the need for any additional training.