Logical GANs: Adversarial Learning through Ehrenfeucht Fraisse Games

GANs promise indistinguishability, logic explains it. We put the two on a budget: a discriminator that can only ``see'' up to a logical depth $k$, and a generator that must look correct to that bounded observer. \textbf{LOGAN} (LOGical GANs) casts the discriminator as a depth-$k$ Ehrenfeucht--Fra\"iss\'e (EF) \emph{Opponent} that searches for small, legible faults (odd cycles, nonplanar crossings, directed bridges), while the generator plays \emph{Builder}, producing samples that admit a $k$-round matching to a target theory $T$. We ship a minimal toolkit -- an EF-probe simulator and MSO-style graph checkers -- and four experiments including real neural GAN training with PyTorch. Beyond verification, we score samples with a \emph{logical loss} that mixes budgeted EF round-resilience with cheap certificate terms, enabling a practical curriculum on depth. Framework validation demonstrates $92\%$--$98\%$ property satisfaction via simulation (Exp.~3), while real neural GAN training achieves $5\%$--$14\%$ improvements on challenging properties and $98\%$ satisfaction on connectivity (matching simulation) through adversarial learning (Exp.~4). LOGAN is a compact, reproducible path toward logic-bounded generation with interpretable failures, proven effectiveness (both simulated and real training), and dials for control.

Node Alertness-Detecting changes in rapidly evolving graphs

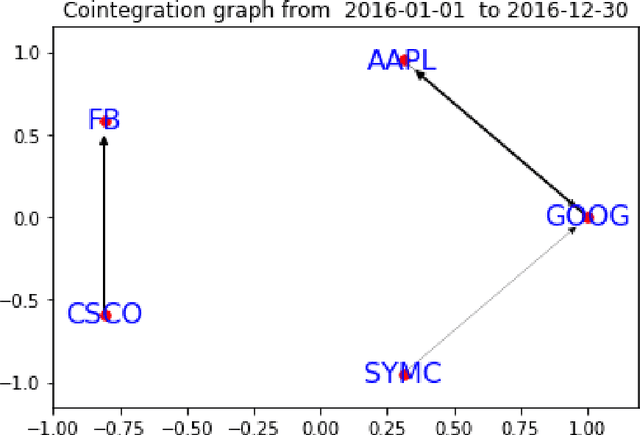
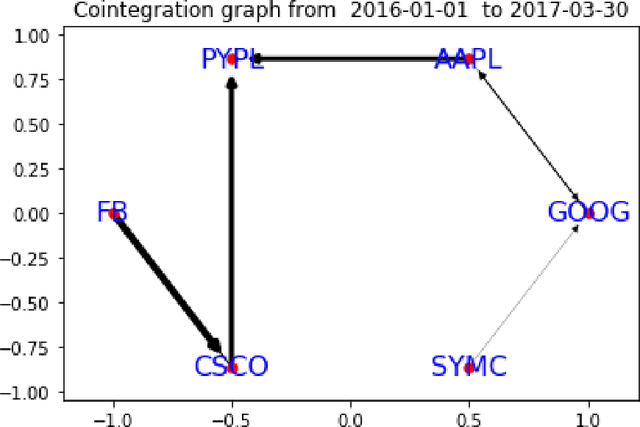
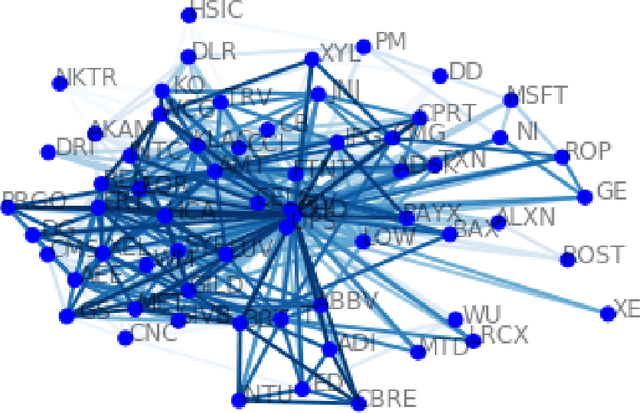
In this article we describe a new approach for detecting changes in rapidly evolving large-scale graphs. The key notion involved is local alertness: nodes monitor change within their neighborhoods at each time step. Here we propose a financial local alertness application for cointegrated stock pairs

Quantum Fuzzy Sets: Blending Fuzzy Set Theory and Quantum Computation

In this article we investigate a way in which quantum computing can be used to extend the class of fuzzy sets. The core idea is to see states of a quantum register as characteristic functions of quantum fuzzy subsets of a given set. As the real unit interval is embedded in the Bloch sphere, every fuzzy set is automatically a quantum fuzzy set. However, a generic quantum fuzzy set can be seen as a (possibly entangled) superposition of many fuzzy sets at once, offering new opportunities for modeling uncertainty. After introducing the main framework of quantum fuzzy set theory, we analyze the standard operations of fuzzification and defuzzification from our viewpoint. We conclude this preliminary paper with a list of possible applications of quantum fuzzy sets to pattern recognition, as well as future directions of pure research in quantum fuzzy set theory.