Exploiting gradients and Hessians in Bayesian optimization and Bayesian quadrature

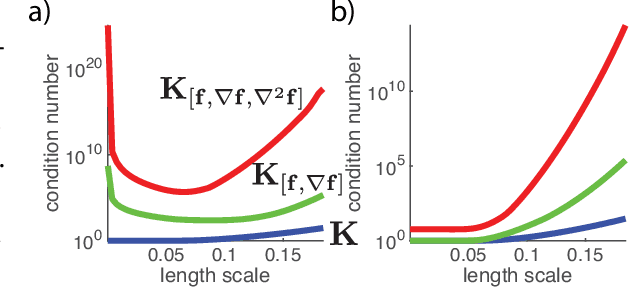
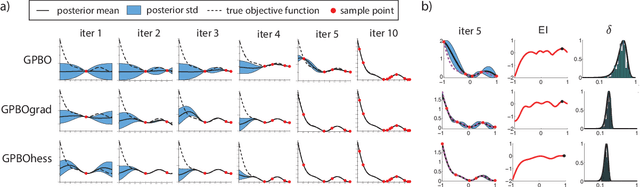
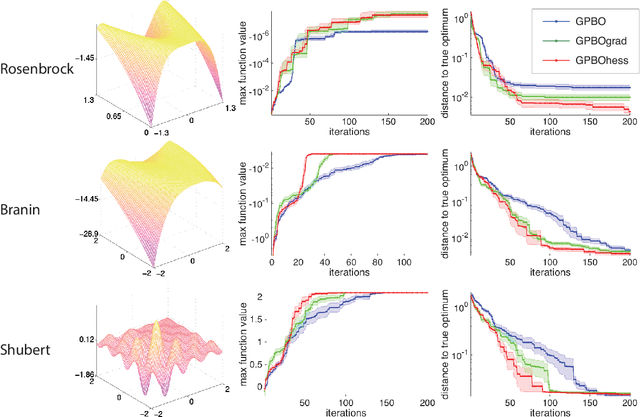
An exciting branch of machine learning research focuses on methods for learning, optimizing, and integrating unknown functions that are difficult or costly to evaluate. A popular Bayesian approach to this problem uses a Gaussian process (GP) to construct a posterior distribution over the function of interest given a set of observed measurements, and selects new points to evaluate using the statistics of this posterior. Here we extend these methods to exploit derivative information from the unknown function. We describe methods for Bayesian optimization (BO) and Bayesian quadrature (BQ) in settings where first and second derivatives may be evaluated along with the function itself. We perform sampling-based inference in order to incorporate uncertainty over hyperparameters, and show that both hyperparameter and function uncertainty decrease much more rapidly when using derivative information. Moreover, we introduce techniques for overcoming ill-conditioning issues that have plagued earlier methods for gradient-enhanced Gaussian processes and kriging. We illustrate the efficacy of these methods using applications to real and simulated Bayesian optimization and quadrature problems, and show that exploting derivatives can provide substantial gains over standard methods.

Matrix-normal models for fMRI analysis

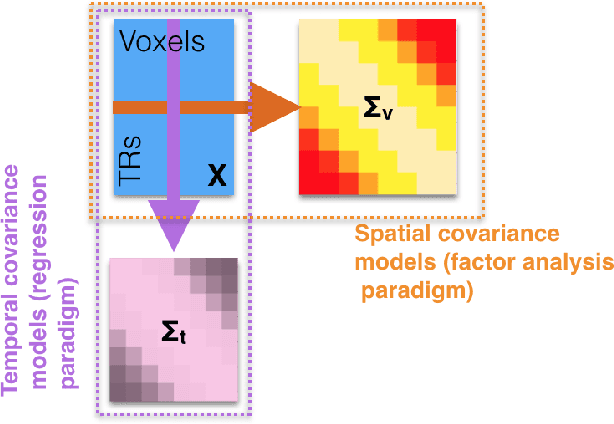
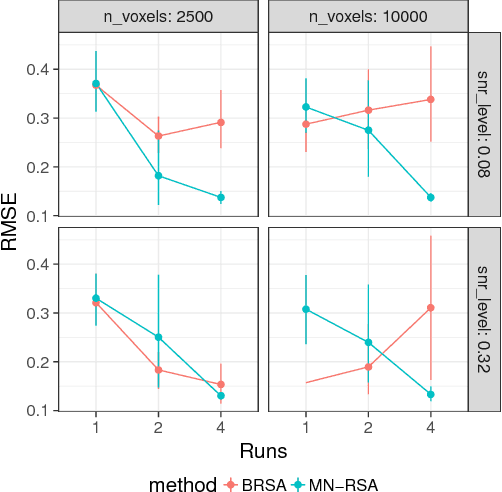
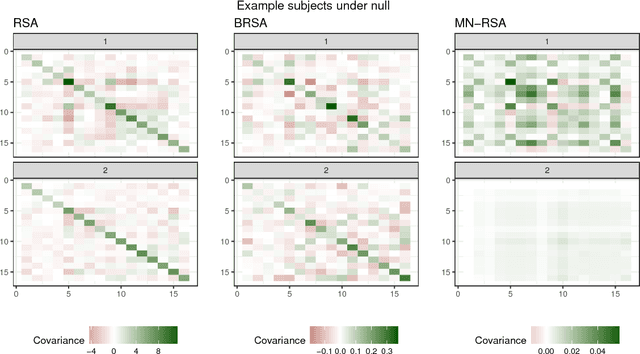
Multivariate analysis of fMRI data has benefited substantially from advances in machine learning. Most recently, a range of probabilistic latent variable models applied to fMRI data have been successful in a variety of tasks, including identifying similarity patterns in neural data (Representational Similarity Analysis and its empirical Bayes variant, RSA and BRSA; Intersubject Functional Connectivity, ISFC), combining multi-subject datasets (Shared Response Mapping; SRM), and mapping between brain and behavior (Joint Modeling). Although these methods share some underpinnings, they have been developed as distinct methods, with distinct algorithms and software tools. We show how the matrix-variate normal (MN) formalism can unify some of these methods into a single framework. In doing so, we gain the ability to reuse noise modeling assumptions, algorithms, and code across models. Our primary theoretical contribution shows how some of these methods can be written as instantiations of the same model, allowing us to generalize them to flexibly modeling structured noise covariances. Our formalism permits novel model variants and improved estimation strategies: in contrast to SRM, the number of parameters for MN-SRM does not scale with the number of voxels or subjects; in contrast to BRSA, the number of parameters for MN-RSA scales additively rather than multiplicatively in the number of voxels. We empirically demonstrate advantages of two new methods derived in the formalism: for MN-RSA, we show up to 10x improvement in runtime, up to 6x improvement in RMSE, and more conservative behavior under the null. For MN-SRM, our method grants a modest improvement to out-of-sample reconstruction while relaxing an orthonormality constraint of SRM. We also provide a software prototyping tool for MN models that can flexibly reuse noise covariance assumptions and algorithms across models.