On the properties of some low-parameter models for color reproduction in terms of spectrum transformations and coverage of a color triangle

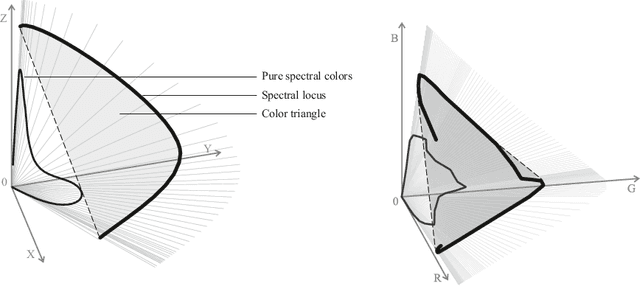
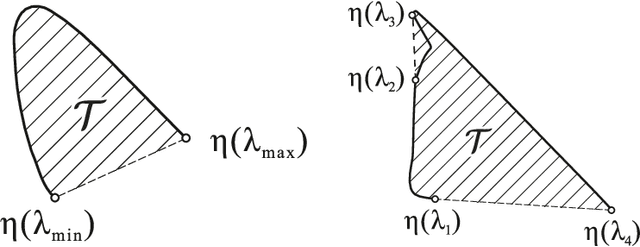
One of the classical approaches to solving color reproduction problems, such as color adaptation or color space transform, is the use of low-parameter spectral models. The strength of this approach is the ability to choose a set of properties that the model should have, be it a large coverage area of a color triangle, an accurate description of the addition or multiplication of spectra, knowing only the tristimulus corresponding to them. The disadvantage is that some of the properties of the mentioned spectral models are confirmed only experimentally. This work is devoted to the theoretical substantiation of various properties of spectral models. In particular, we prove that the banded model is the only model that simultaneously possesses the properties of closure under addition and multiplication. We also show that the Gaussian model is the limiting case of the von Mises model and prove that the set of protomers of the von Mises model unambiguously covers the color triangle in both the case of convex and non-convex spectral locus.