Miguel Carreira-Perpinan
UC Merced
Partial-Hessian Strategies for Fast Learning of Nonlinear Embeddings
Jun 18, 2012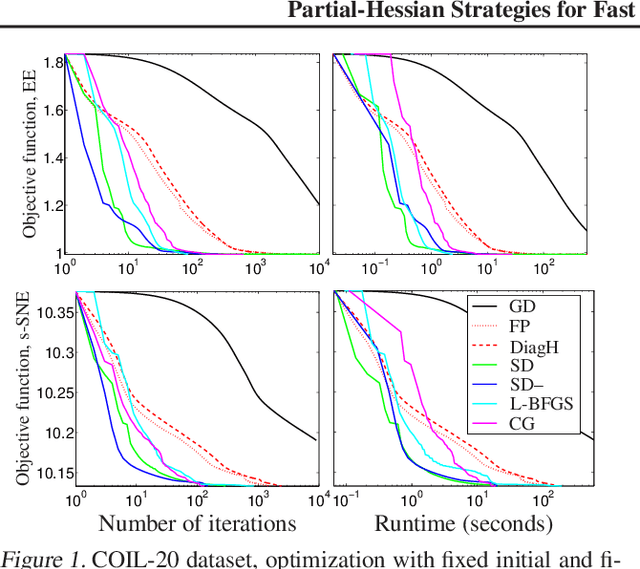
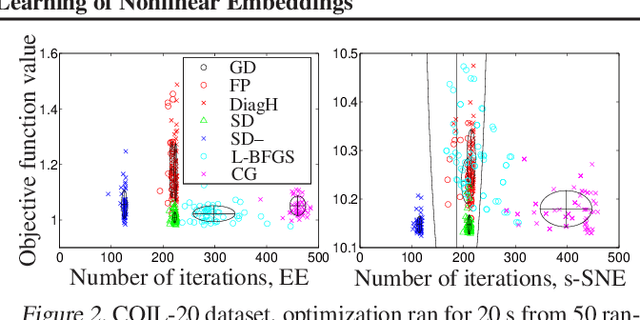
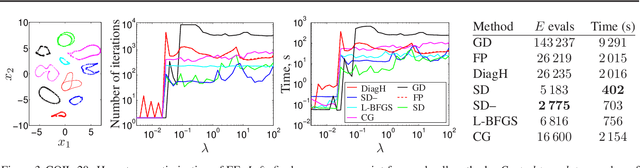
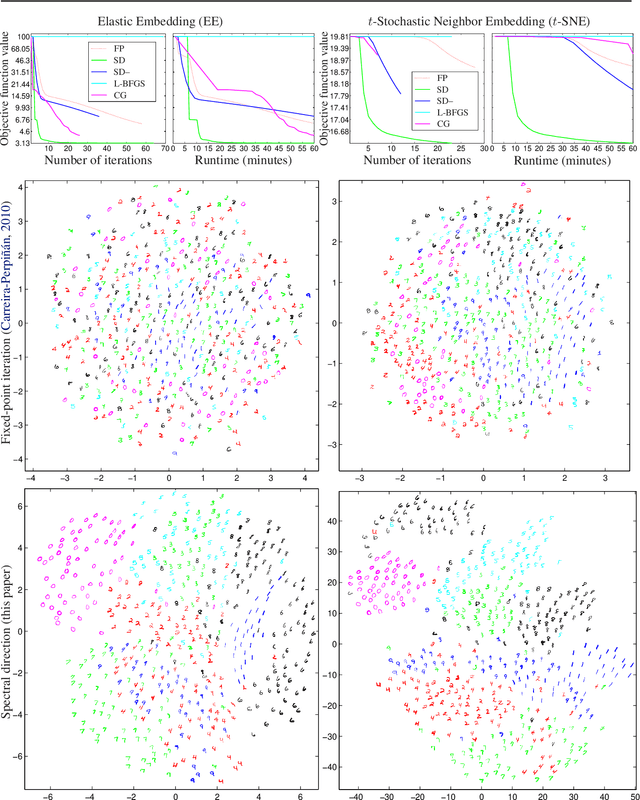
Abstract:Stochastic neighbor embedding (SNE) and related nonlinear manifold learning algorithms achieve high-quality low-dimensional representations of similarity data, but are notoriously slow to train. We propose a generic formulation of embedding algorithms that includes SNE and other existing algorithms, and study their relation with spectral methods and graph Laplacians. This allows us to define several partial-Hessian optimization strategies, characterize their global and local convergence, and evaluate them empirically. We achieve up to two orders of magnitude speedup over existing training methods with a strategy (which we call the spectral direction) that adds nearly no overhead to the gradient and yet is simple, scalable and applicable to several existing and future embedding algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge