Light-Weight Diffusion Multiplier and Uncertainty Quantification for Fourier Neural Operators

Operator learning is a powerful paradigm for solving partial differential equations, with Fourier Neural Operators serving as a widely adopted foundation. However, FNOs face significant scalability challenges due to overparameterization and offer no native uncertainty quantification -- a key requirement for reliable scientific and engineering applications. Instead, neural operators rely on post hoc UQ methods that ignore geometric inductive biases. In this work, we introduce DINOZAUR: a diffusion-based neural operator parametrization with uncertainty quantification. Inspired by the structure of the heat kernel, DINOZAUR replaces the dense tensor multiplier in FNOs with a dimensionality-independent diffusion multiplier that has a single learnable time parameter per channel, drastically reducing parameter count and memory footprint without compromising predictive performance. By defining priors over those time parameters, we cast DINOZAUR as a Bayesian neural operator to yield spatially correlated outputs and calibrated uncertainty estimates. Our method achieves competitive or superior performance across several PDE benchmarks while providing efficient uncertainty quantification.

Geometric fluid approximation for general continuous-time Markov chains

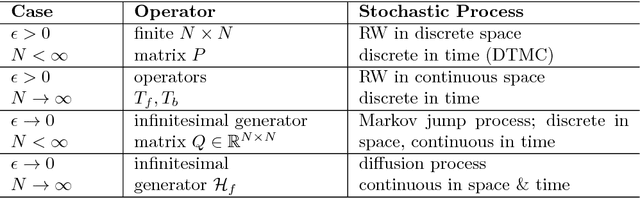
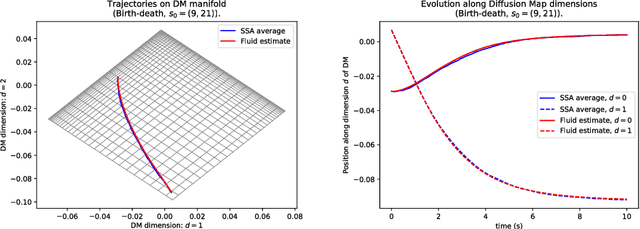
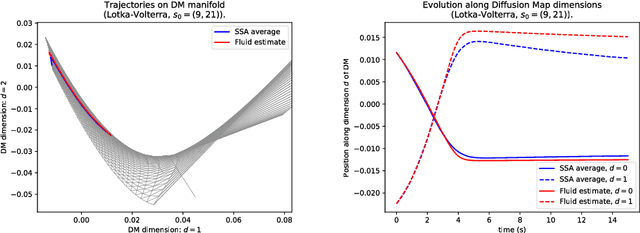
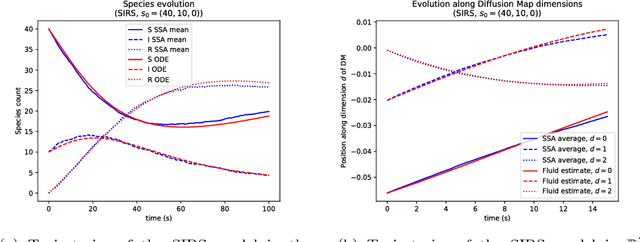
Fluid approximations have seen great success in approximating the macro-scale behaviour of Markov systems with a large number of discrete states. However, these methods rely on the continuous-time Markov chain (CTMC) having a particular population structure which suggests a natural continuous state-space endowed with a dynamics for the approximating process. We construct here a general method based on spectral analysis of the transition matrix of the CTMC, without the need for a population structure. Specifically, we use the popular manifold learning method of diffusion maps to analyse the transition matrix as the operator of a hidden continuous process. An embedding of states in a continuous space is recovered, and the space is endowed with a drift vector field inferred via Gaussian process regression. In this manner, we construct an ODE whose solution approximates the evolution of the CTMC mean, mapped onto the continuous space (known as the fluid limit).

Property-driven State-Space Coarsening for Continuous Time Markov Chains

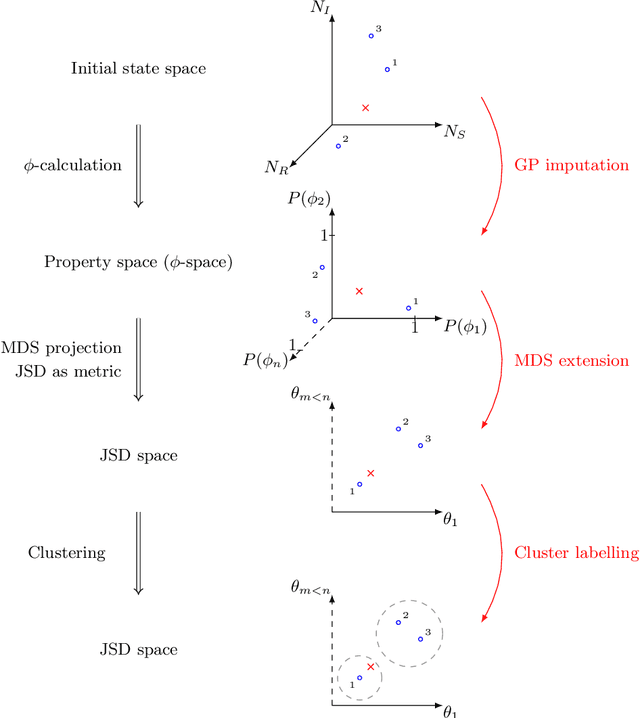
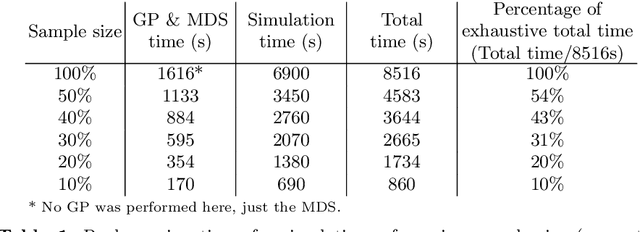
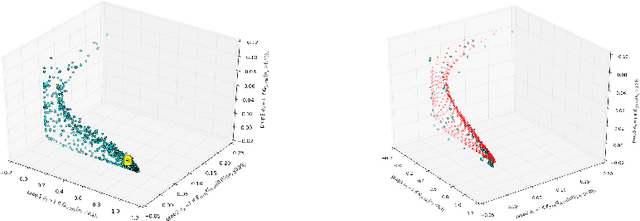
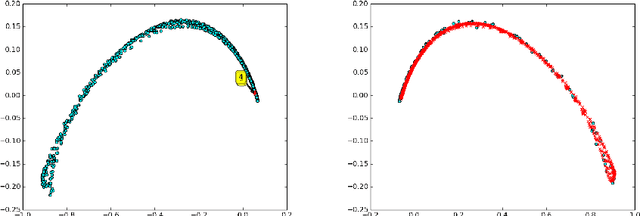
Dynamical systems with large state-spaces are often expensive to thoroughly explore experimentally. Coarse-graining methods aim to define simpler systems which are more amenable to analysis and exploration; most current methods, however, focus on a priori state aggregation based on similarities in transition rates, which is not necessarily reflected in similar behaviours at the level of trajectories. We propose a way to coarsen the state-space of a system which optimally preserves the satisfaction of a set of logical specifications about the system's trajectories. Our approach is based on Gaussian Process emulation and Multi-Dimensional Scaling, a dimensionality reduction technique which optimally preserves distances in non-Euclidean spaces. We show how to obtain low-dimensional visualisations of the system's state-space from the perspective of properties' satisfaction, and how to define macro-states which behave coherently with respect to the specifications. Our approach is illustrated on a non-trivial running example, showing promising performance and high computational efficiency.