A Physics Informed Machine Learning Framework for Optimal Sensor Placement and Parameter Estimation

Parameter estimation remains a challenging task across many areas of engineering. Because data acquisition can often be costly, limited, or prone to inaccuracies (noise, uncertainty) it is crucial to identify sensor configurations that provide the maximum amount of information about the unknown parameters, in particular for the case of distributed-parameter systems, where spatial variations are important. Physics-Informed Neural Networks (PINNs) have recently emerged as a powerful machine-learning (ML) tool for parameter estimation, particularly in cases with sparse or noisy measurements, overcoming some of the limitations of traditional optimization-based and Bayesian approaches. Despite the widespread use of PINNs for solving inverse problems, relatively little attention has been given to how their performance depends on sensor placement. This study addresses this gap by introducing a comprehensive PINN-based framework that simultaneously tackles optimal sensor placement and parameter estimation. Our approach involves training a PINN model in which the parameters of interest are included as additional inputs. This enables the efficient computation of sensitivity functions through automatic differentiation, which are then used to determine optimal sensor locations exploiting the D-optimality criterion. The framework is validated on two illustrative distributed-parameter reaction-diffusion-advection problems of increasing complexity. The results demonstrate that our PINNs-based methodology consistently achieves higher accuracy compared to parameter values estimated from intuitively or randomly selected sensor positions.

Limits of Entrainment of Circadian Neuronal Networks

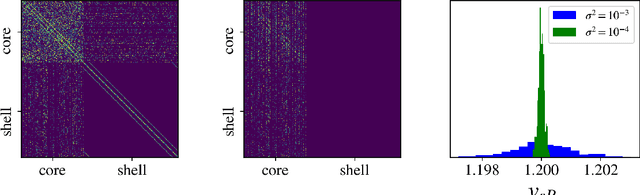
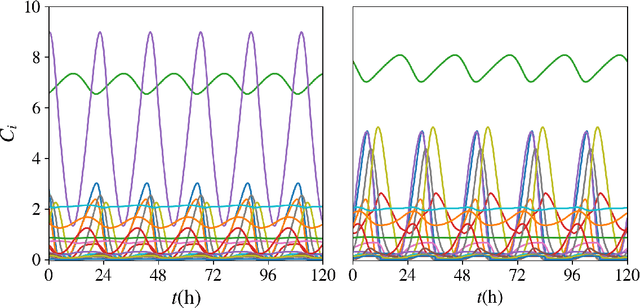
Circadian rhythmicity lies at the center of various important physiological and behavioral processes in mammals, such as sleep, metabolism, homeostasis, mood changes and more. It has been shown that this rhythm arises from self-sustained biomolecular oscillations of a neuronal network located in the Suprachiasmatic Nucleus (SCN). Under normal circumstances, this network remains synchronized to the day-night cycle due to signaling from the retina. Misalignment of these neuronal oscillations with the external light signal can disrupt numerous physiological functions and take a long-lasting toll on health and well-being. In this work, we study a modern computational neuroscience model to determine the limits of circadian synchronization to external light signals of different frequency and duty cycle. We employ a matrix-free approach to locate periodic steady states of the high-dimensional model for various driving conditions. Our algorithmic pipeline enables numerical continuation and construction of bifurcation diagrams w.r.t. forcing parameters. We computationally explore the effect of heterogeneity in the circadian neuronal network, as well as the effect of corrective therapeutic interventions, such as that of the drug molecule Longdaysin. Lastly, we employ unsupervised learning to construct a data-driven embedding space for representing neuronal heterogeneity.