Using Salient Object Detection to Identify Manipulative Cookie Banners that Circumvent GDPR

The main goal of this paper is to study how often cookie banners that comply with the General Data Protection Regulation (GDPR) contain aesthetic manipulation, a design tactic to draw users' attention to the button that permits personal data sharing. As a byproduct of this goal, we also evaluate how frequently the banners comply with GDPR and the recommendations of national data protection authorities regarding banner designs. We visited 2,579 websites and identified the type of cookie banner implemented. Although 45% of the relevant websites have fully compliant banners, we found aesthetic manipulation on 38% of the compliant banners. Unlike prior studies of aesthetic manipulation, we use a computer vision model for salient object detection to measure how salient (i.e., attention-drawing) each banner element is. This enables the discovery of new types of aesthetic manipulation (e.g., button placement), and leads us to conclude that aesthetic manipulation is more common than previously reported (38% vs 27% of banners). To study the effects of user and/or website location on cookie banner design, we include websites within the European Union (EU), where privacy regulation enforcement is more stringent, and websites outside the EU. We visited websites from IP addresses in the EU and from IP addresses in the United States (US). We find that 13.9% of EU websites change their banner design when the user is from the US, and EU websites are roughly 48.3% more likely to use aesthetic manipulation than non-EU websites, highlighting their innovative responses to privacy regulation.

Uncertainty estimation in Deep Learning for Panoptic segmentation

As deep learning-based computer vision algorithms continue to improve and advance the state of the art, their robustness to real-world data continues to lag their performance on datasets. This makes it difficult to bring an algorithm from the lab to the real world. Ensemble-based uncertainty estimation approaches such as Monte Carlo Dropout have been successfully used in many applications in an attempt to address this robustness issue. Unfortunately, it is not always clear if such ensemble-based approaches can be applied to a new problem domain. This is the case with panoptic segmentation, where the structure of the problem and architectures designed to solve it means that unlike image classification or even semantic segmentation, the typical solution of using a mean across samples cannot be directly applied. In this paper, we demonstrate how ensemble-based uncertainty estimation approaches such as Monte Carlo Dropout can be used in the panoptic segmentation domain with no changes to an existing network, providing both improved performance and more importantly a better measure of uncertainty for predictions made by the network. Results are demonstrated quantitatively and qualitatively on the COCO, KITTI-STEP and VIPER datasets.

Adjoint-aided inference of Gaussian process driven differential equations

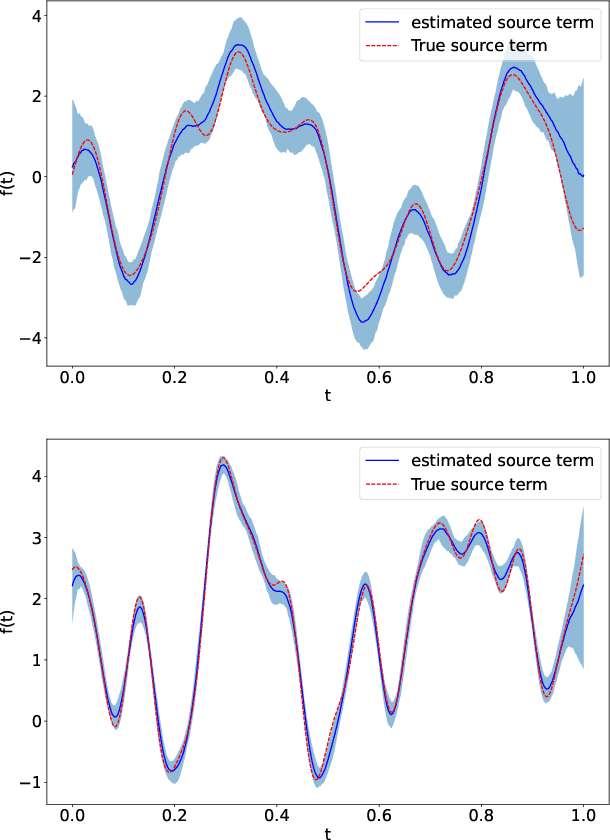
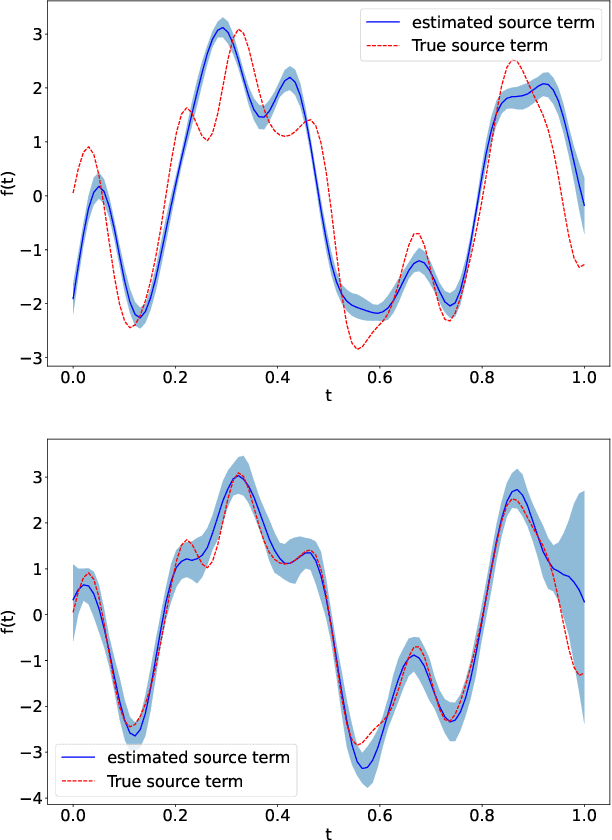
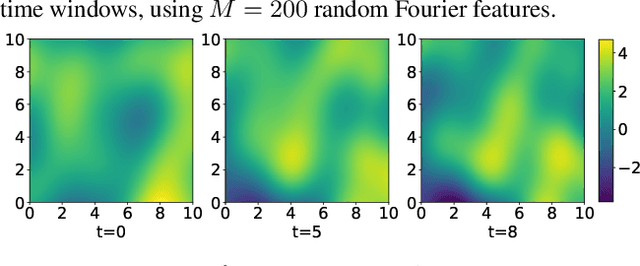
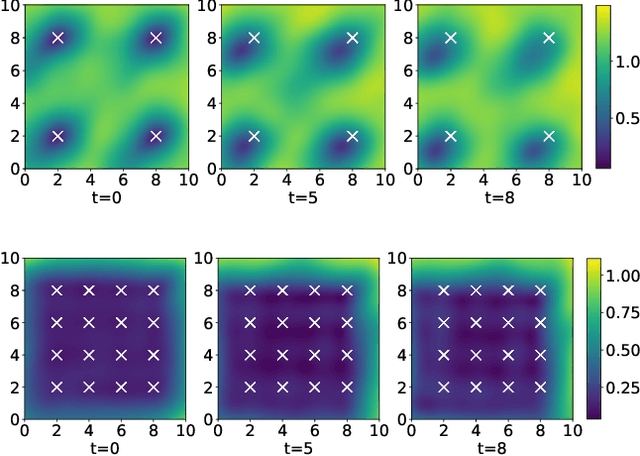
Linear systems occur throughout engineering and the sciences, most notably as differential equations. In many cases the forcing function for the system is unknown, and interest lies in using noisy observations of the system to infer the forcing, as well as other unknown parameters. In differential equations, the forcing function is an unknown function of the independent variables (typically time and space), and can be modelled as a Gaussian process (GP). In this paper we show how the adjoint of a linear system can be used to efficiently infer forcing functions modelled as GPs, after using a truncated basis expansion of the GP kernel. We show how exact conjugate Bayesian inference for the truncated GP can be achieved, in many cases with substantially lower computation than would be required using MCMC methods. We demonstrate the approach on systems of both ordinary and partial differential equations, and by testing on synthetic data, show that the basis expansion approach approximates well the true forcing with a modest number of basis vectors. Finally, we show how to infer point estimates for the non-linear model parameters, such as the kernel length-scales, using Bayesian optimisation.

Amanuensis: The Programmer's Apprentice

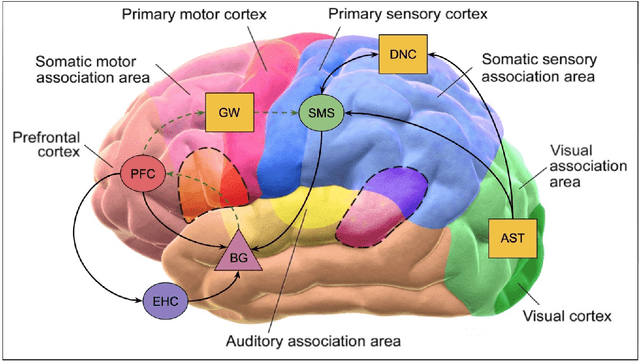
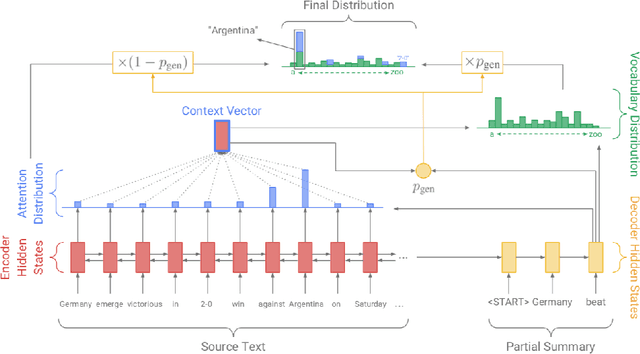
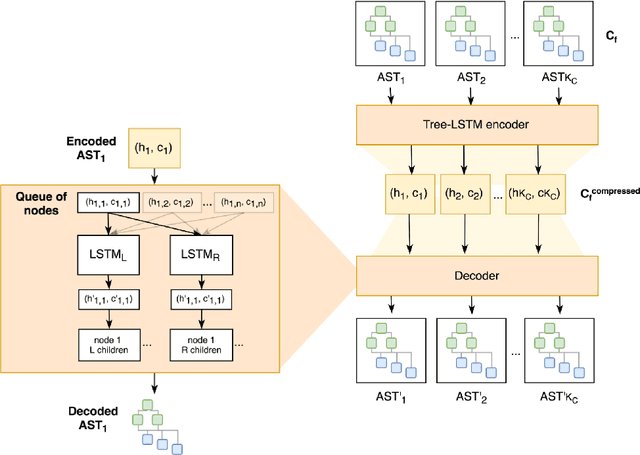
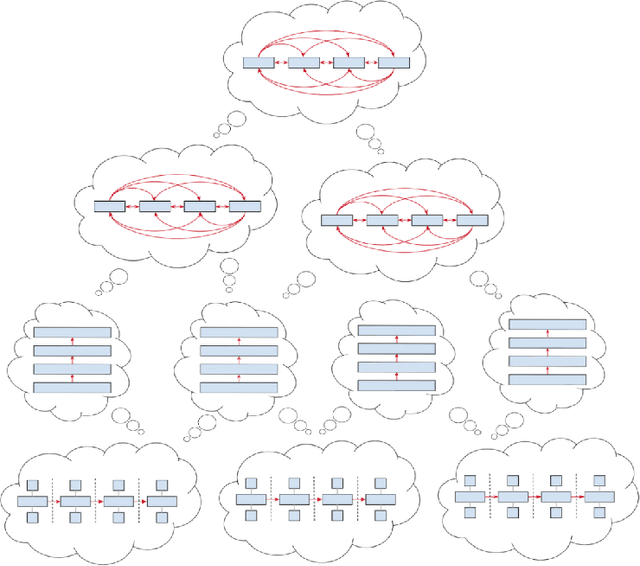
This document provides an overview of the material covered in a course taught at Stanford in the spring quarter of 2018. The course draws upon insight from cognitive and systems neuroscience to implement hybrid connectionist and symbolic reasoning systems that leverage and extend the state of the art in machine learning by integrating human and machine intelligence. As a concrete example we focus on digital assistants that learn from continuous dialog with an expert software engineer while providing initial value as powerful analytical, computational and mathematical savants. Over time these savants learn cognitive strategies (domain-relevant problem solving skills) and develop intuitions (heuristics and the experience necessary for applying them) by learning from their expert associates. By doing so these savants elevate their innate analytical skills allowing them to partner on an equal footing as versatile collaborators - effectively serving as cognitive extensions and digital prostheses, thereby amplifying and emulating their human partner's conceptually-flexible thinking patterns and enabling improved access to and control over powerful computing resources.