Dataset of polarimetric images of mechanically generated water surface waves coupled with surface elevation records by wave gauges linear array

Effective spatio-temporal measurements of water surface elevation (water waves) in laboratory experiments are essential for scientific and engineering research. Existing techniques are often cumbersome, computationally heavy and generally suffer from limited wavenumber/frequency response. To address these challenges a novel method was developed, using polarization filter equipped camera as the main sensor and Machine Learning (ML) algorithms for data processing [1,2]. The developed method training and evaluation was based on in-house made supervised dataset. Here we present this supervised dataset of polarimetric images of the water surface coupled with the water surface elevation measurements made by a linear array of resistance-type wave gauges (WG). The water waves were mechanically generated in a laboratory waves basin, and the polarimetric images were captured under an artificial light source. Meticulous camera and WGs calibration and instruments synchronization supported high spatio-temporal resolution. The data set covers several wavefield conditions, from simple monochromatic wave trains of various steepness, to irregular wavefield of JONSWAP prescribed spectral shape and several wave breaking scenarios. The dataset contains measurements repeated in several camera positions relative to the wave field propagation direction.

Wave (from) Polarized Light Learning (WPLL) method: high resolution spatio-temporal measurements of water surface waves in laboratory setups

Effective spatio-temporal measurements of water surface elevation (water waves) in laboratory experiments are crucial for scientific and engineering research. Existing techniques are often cumbersome, computationally heavy and generally suffer from limitations in wavenumber/frequency response. To address these challenges, we propose Wave (from) Polarized Light Learning (WPLL), a learning based remote sensing method for laboratory implementation, capable of inferring surface elevation and slope maps in high resolution. The method uses the polarization properties of light reflected from the water surface. The WPLL uses a deep neural network (DNN) model that approximates the water surface slopes from the polarized light intensities. Once trained on simple monochromatic wave trains, the WPLL is capable of producing high-resolution and accurate 2D reconstruction of the water surface slopes and elevation in a variety of irregular wave fields. The method's robustness is demonstrated by showcasing its high wavenumber/frequency response, its ability to reconstruct wave fields propagating at arbitrary angles relative to the camera optical axis, and its computational efficiency. This developed methodology is an accurate and cost-effective near-real time remote sensing tool for laboratory water surface waves measurements, setting the path for upscaling to open sea application for research, monitoring, and short-time forecasting.

Metric Convolutions: A Unifying Theory to Adaptive Convolutions

Standard convolutions are prevalent in image processing and deep learning, but their fixed kernel design limits adaptability. Several deformation strategies of the reference kernel grid have been proposed. Yet, they lack a unified theoretical framework. By returning to a metric perspective for images, now seen as two-dimensional manifolds equipped with notions of local and geodesic distances, either symmetric (Riemannian metrics) or not (Finsler metrics), we provide a unifying principle: the kernel positions are samples of unit balls of implicit metrics. With this new perspective, we also propose metric convolutions, a novel approach that samples unit balls from explicit signal-dependent metrics, providing interpretable operators with geometric regularisation. This framework, compatible with gradient-based optimisation, can directly replace existing convolutions applied to either input images or deep features of neural networks. Metric convolutions typically require fewer parameters and provide better generalisation. Our approach shows competitive performance in standard denoising and classification tasks.

From Compass and Ruler to Convolution and Nonlinearity: On the Surprising Difficulty of Understanding a Simple CNN Solving a Simple Geometric Estimation Task

Neural networks are omnipresent, but remain poorly understood. Their increasing complexity and use in critical systems raises the important challenge to full interpretability. We propose to address a simple well-posed learning problem: estimating the radius of a centred pulse in a one-dimensional signal or of a centred disk in two-dimensional images using a simple convolutional neural network. Surprisingly, understanding what trained networks have learned is difficult and, to some extent, counter-intuitive. However, an in-depth theoretical analysis in the one-dimensional case allows us to comprehend constraints due to the chosen architecture, the role of each filter and of the nonlinear activation function, and every single value taken by the weights of the model. Two fundamental concepts of neural networks arise: the importance of invariance and of the shape of the nonlinear activation functions.

Assessing hierarchies by their consistent segmentations

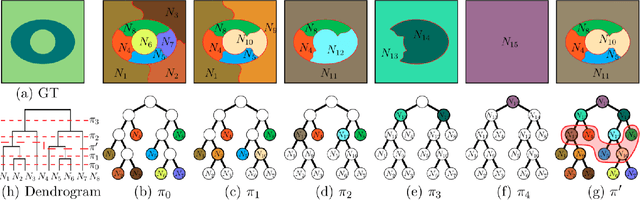
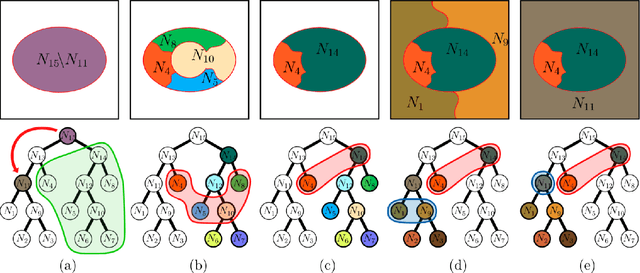
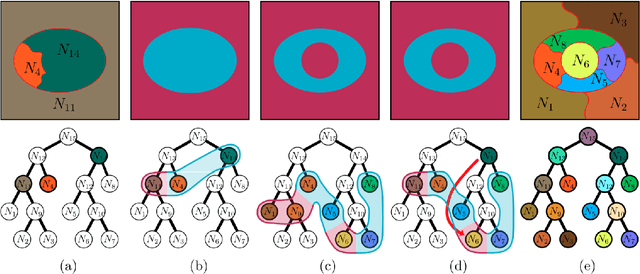
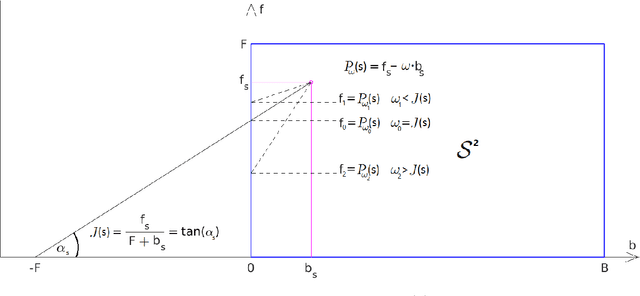
Recent segmentation approaches start by creating a hierarchy of nested image partitions, and then specify a segmentation from it, usually, by choosing one horizontal cut. Our first contribution is to describe several different ways, some of them new, for specifying segmentations using the hierarchy regions. Then we consider the best hierarchy-induced segmentation, in which the segments are specified by a limited number, k, of hierarchy nodes/regions. The number of hierarchy-induced segmentations grows exponentially with the hierarchy size, implying that exhaustive search is unfeasible. We focus on a common quality measure, the Jaccard index (known also as IoU). Optimizing the Jaccard index is highly nontrivial. Yet, we propose an efficient optimization * This work was done when the first author was with the Math dept. Technion, Israel.

On the Minimal Recognizable Image Patch

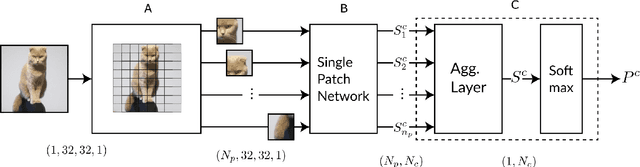
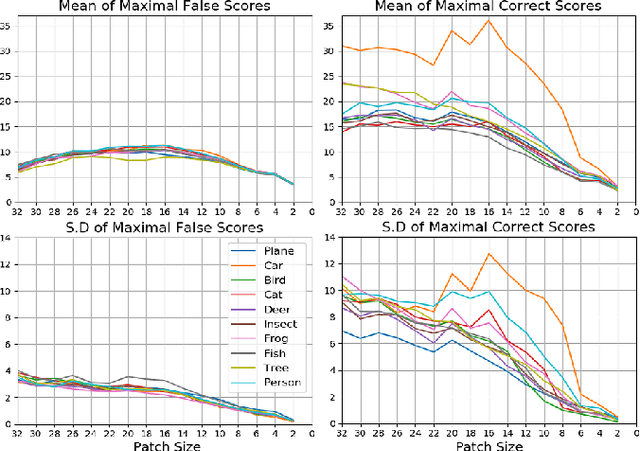
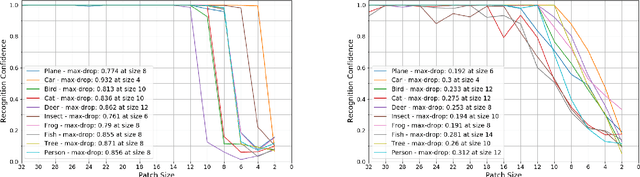
In contrast to human vision, common recognition algorithms often fail on partially occluded images. We propose characterizing, empirically, the algorithmic limits by finding a minimal recognizable patch (MRP) that is by itself sufficient to recognize the image. A specialized deep network allows us to find the most informative patches of a given size, and serves as an experimental tool. A human vision study recently characterized related (but different) minimally recognizable configurations (MIRCs) [1], for which we specify computational analogues (denoted cMIRCs). The drop in human decision accuracy associated with size reduction of these MIRCs is substantial and sharp. Interestingly, such sharp reductions were also found for the computational versions we specified.

DPDist : Comparing Point Clouds Using Deep Point Cloud Distance

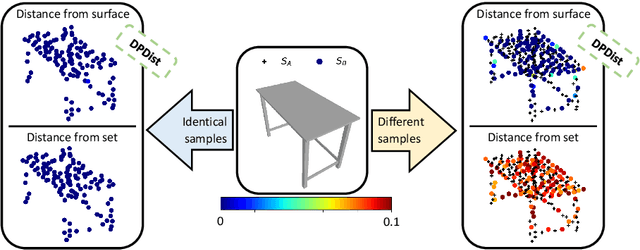
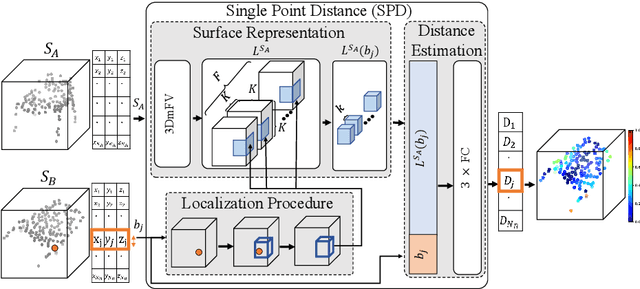
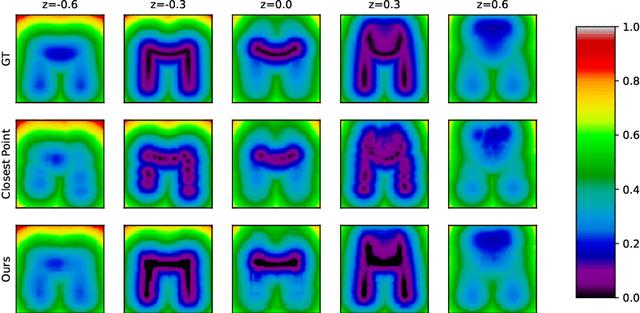
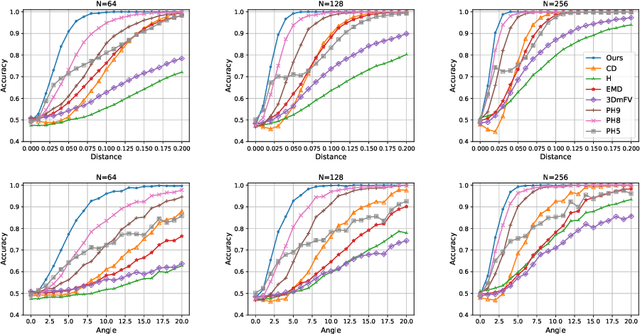
We introduce a new deep learning method for point cloud comparison. Our approach, named Deep Point Cloud Distance (DPDist), measures the distance between the points in one cloud and the estimated surface from which the other point cloud is sampled. The surface is estimated locally and efficiently using the 3D modified Fisher vector representation. The local representation reduces the complexity of the surface, enabling efficient and effective learning, which generalizes well between object categories. We test the proposed distance in challenging tasks, such as similar object comparison and registration, and show that it provides significant improvements over commonly used distances such as Chamfer distance, Earth mover's distance, and others.

Enhancing Generic Segmentation with Learned Region Representations

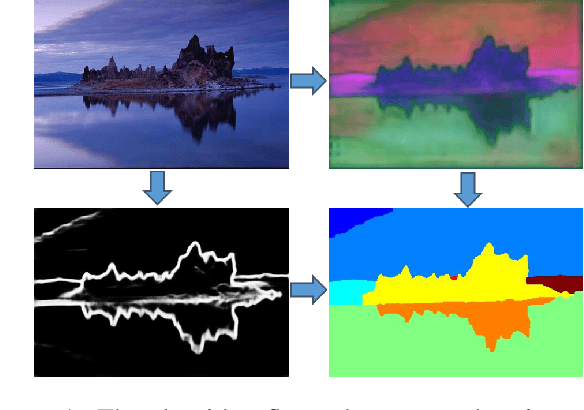
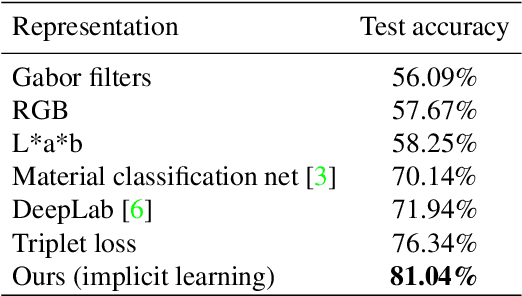
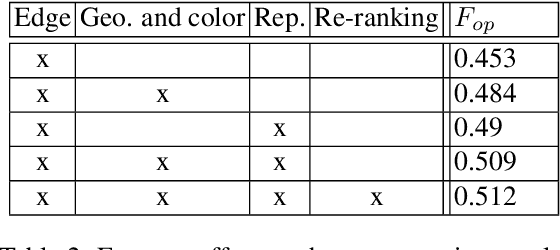
Current successful approaches for generic (non-semantic) segmentation rely mostly on edge detection and have leveraged the strengths of deep learning mainly by improving the edge detection stage in the algorithmic pipeline. This is in contrast to semantic and instance segmentation, where deep learning has made a dramatic affect and DNNs are applied directly to generate pixel-wise segment representations. We propose a new method for learning a pixelwise representation that reflects segment relatedness. This representation is combined with an edge map to yield a new segmentation algorithm. We show that the representations themselves achieve state-of-the-art segment similarity scores. Moreover, the proposed, combined segmentation algorithm provides results that are either the state of the art or improve it, for most quality measures.

Learning Pixel Representations for Generic Segmentation

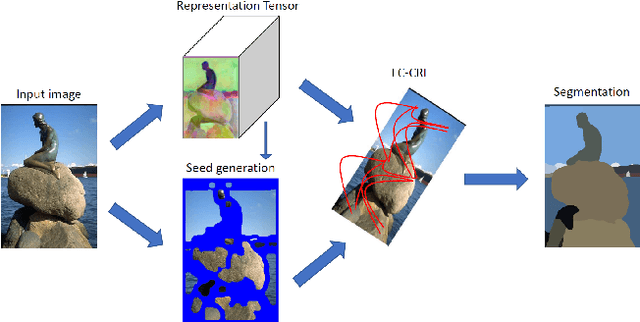
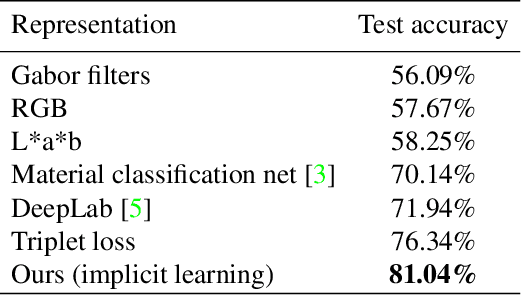
Deep learning approaches to generic (non-semantic) segmentation have so far been indirect and relied on edge detection. This is in contrast to semantic segmentation, where DNNs are applied directly. We propose an alternative approach called Deep Generic Segmentation (DGS) and try to follow the path used for semantic segmentation. Our main contribution is a new method for learning a pixel-wise representation that reflects segment relatedness. This representation is combined with a CRF to yield the segmentation algorithm. We show that we are able to learn meaningful representations that improve segmentation quality and that the representations themselves achieve state-of-the-art segment similarity scores. The segmentation results are competitive and promising.

Seeing Things in Random-Dot Videos

The human visual system correctly groups features and interprets videos displaying non persistent and noisy random-dot data induced by imaging natural dynamic scenes. Remarkably, this happens even if perception completely fails when the same information is presented frame by frame. We study this property of surprising dynamic perception with the first goal of proposing a new detection and spatio-temporal grouping algorithm for such signals when, per frame, the information on objects is both random and sparse. The striking similarity in performance of the algorithm to the perception by human observers, as witnessed by a series of psychophysical experiments that were performed, leads us to see in it a simple computational Gestalt model of human perception based on temporal integration and statistical tests of unlikeliness, the a contrario framework.