The Exact Determinant of a Specific Class of Sparse Positive Definite Matrices

For a specific class of sparse Gaussian graphical models, we provide a closed-form solution for the determinant of the covariance matrix. In our framework, the graphical interaction model (i.e., the covariance selection model) is equal to replacement product of $\mathcal{K}_{n}$ and $\mathcal{K}_{n-1}$, where $\mathcal{K}_n$ is the complete graph with $n$ vertices. Our analysis is based on taking the Fourier transform of the local factors of the model, which can be viewed as an application of the Normal Factor Graph Duality Theorem and holographic algorithms. The closed-form expression is obtained by applying the Matrix Determinant Lemma on the transformed graphical model. In this context, we will also define a notion of equivalence between two Gaussian graphical models.

Mappings for Marginal Probabilities with Applications to Models in Statistical Physics

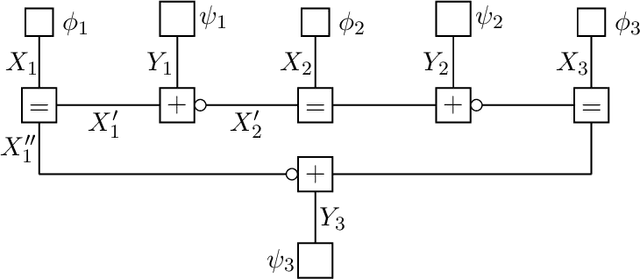
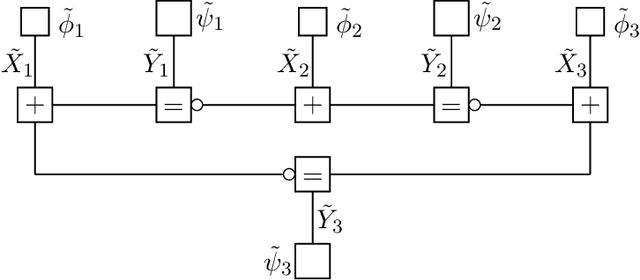
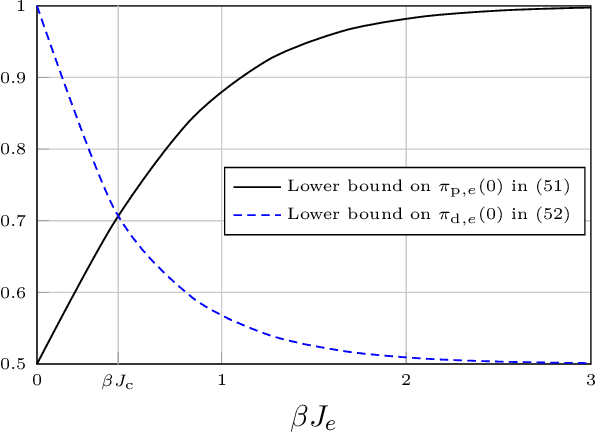
We present local mappings that relate the marginal probabilities of a global probability mass function represented by its primal normal factor graph to the corresponding marginal probabilities in its dual normal factor graph. The mapping is based on the Fourier transform of the local factors of the models. Details of the mapping are provided for the Ising model, where it is proved that the local extrema of the fixed points are attained at the phase transition of the two-dimensional nearest-neighbor Ising model. The results are further extended to the Potts model, to the clock model, and to Gaussian Markov random fields. By employing the mapping, we can transform simultaneously all the estimated marginal probabilities from the dual domain to the primal domain (and vice versa), which is advantageous if estimating the marginals can be carried out more efficiently in the dual domain. An example of particular significance is the ferromagnetic Ising model in a positive external magnetic field. For this model, there exists a rapidly mixing Markov chain (called the subgraphs--world process) to generate configurations in the dual normal factor graph of the model. Our numerical experiments illustrate that the proposed procedure can provide more accurate estimates of marginal probabilities of a global probability mass function in various settings.

Duality for Continuous Graphical Models

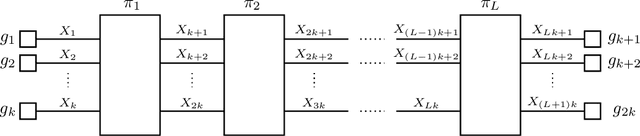
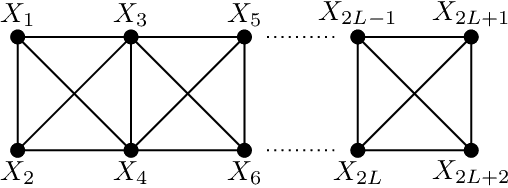
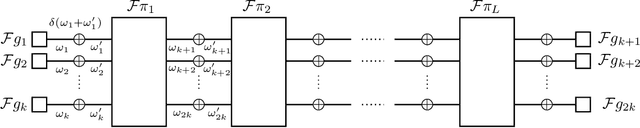
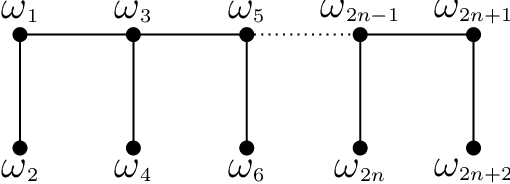
The dual normal factor graph and the factor graph duality theorem have been considered for discrete graphical models. In this paper, we show an application of the factor graph duality theorem to continuous graphical models. Specifically, we propose a method to solve exactly the Gaussian graphical models defined on the ladder graph if certain conditions on the local covariance matrices are satisfied. Unlike the conventional approaches, the efficiency of the method depends on the position of the zeros in the local covariance matrices. The method and details of the dualization are illustrated on two toy examples.

Marginal Densities, Factor Graph Duality, and High-Temperature Series Expansions

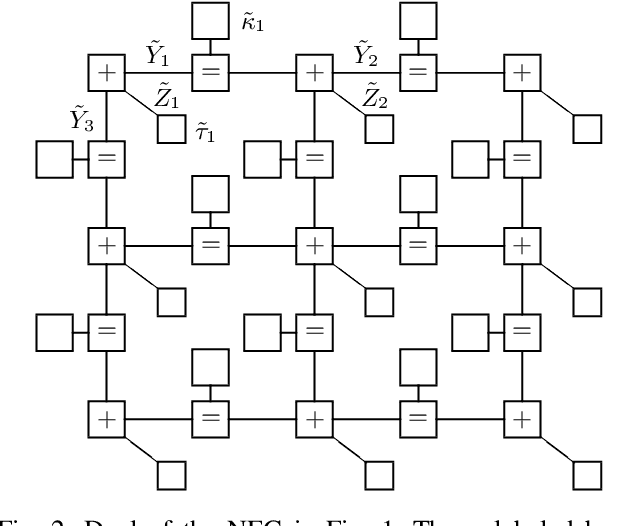
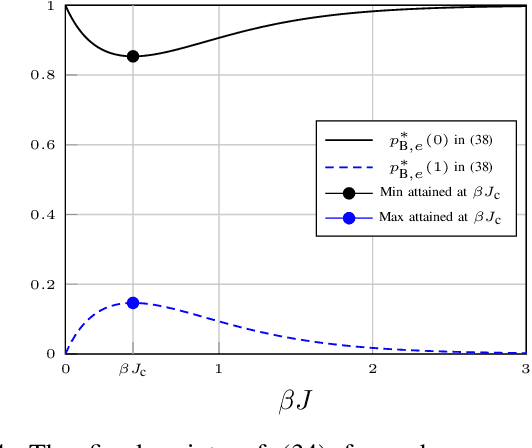
We prove that the marginals densities of a primal normal factor graph and the corresponding marginal densities of its dual normal factor graph are related via local mappings. The mapping relies on no assumptions on the size, on the topology, or on the parameters of the graphical model. The mapping provides us with a simple procedure to transform simultaneously the estimated marginals from one domain to the other, which is particularly useful when such computations can be carried out more efficiently in one of the domains. In the case of the Ising model, valid configurations in the dual normal factor graph of the model coincide with the terms that appear in the high-temperature series expansion of the partition function. The subgraphs-world process (as a rapidly mixing Markov chain) can therefore be employed to draw samples according to the global probability mass function of the dual normal factor graph of ferromagnetic Ising models.