Benignity of loss landscape with weight decay requires both large overparametrization and initialization

The optimization of neural networks under weight decay remains poorly understood from a theoretical standpoint. While weight decay is standard practice in modern training procedures, most theoretical analyses focus on unregularized settings. In this work, we investigate the loss landscape of the $\ell_2$-regularized training loss for two-layer ReLU networks. We show that the landscape becomes benign -- i.e., free of spurious local minima -- under large overparametrization, specifically when the network width $m$ satisfies $m \gtrsim \min(n^d, 2^n)$, where $n$ is the number of data points and $d$ the input dimension. More precisely in this regime, almost all constant activation regions contain a global minimum and no spurious local minima. We further show that this level of overparametrization is not only sufficient but also necessary via the example of orthogonal data. Finally, we demonstrate that such loss landscape results primarily hold relevance in the large initialization regime. In contrast, for small initializations -- corresponding to the feature learning regime -- optimization can still converge to spurious local minima, despite the global benignity of the landscape.

Learning a Neuron by a Shallow ReLU Network: Dynamics and Implicit Bias for Correlated Inputs

We prove that, for the fundamental regression task of learning a single neuron, training a one-hidden layer ReLU network of any width by gradient flow from a small initialisation converges to zero loss and is implicitly biased to minimise the rank of network parameters. By assuming that the training points are correlated with the teacher neuron, we complement previous work that considered orthogonal datasets. Our results are based on a detailed non-asymptotic analysis of the dynamics of each hidden neuron throughout the training. We also show and characterise a surprising distinction in this setting between interpolator networks of minimal rank and those of minimal Euclidean norm. Finally we perform a range of numerical experiments, which corroborate our theoretical findings.

Adversarial Reprogramming Revisited

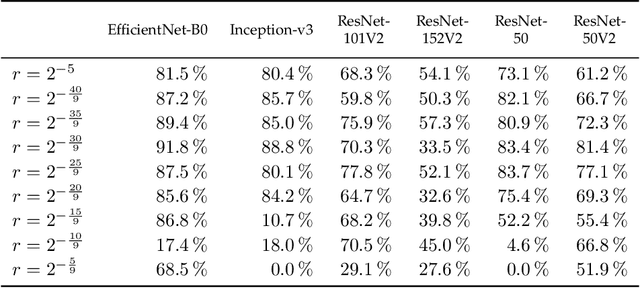
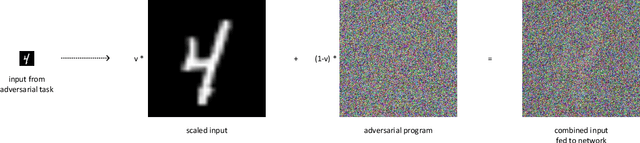
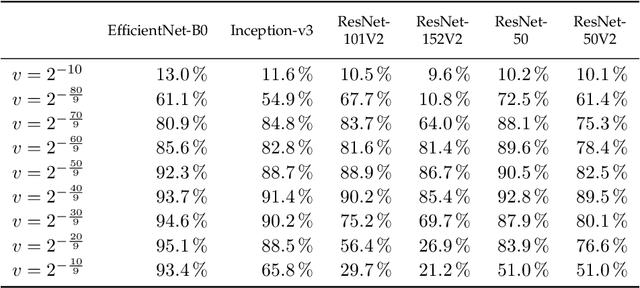
Adversarial reprogramming, introduced by Elsayed, Goodfellow, and Sohl-Dickstein, seeks to repurpose a neural network to perform a different task, by manipulating its input without modifying its weights. We prove that two-layer ReLU neural networks with random weights can be adversarially reprogrammed to achieve arbitrarily high accuracy on Bernoulli data models over hypercube vertices, provided the network width is no greater than its input dimension. We also substantially strengthen a recent result of Phuong and Lampert on directional convergence of gradient flow, and obtain as a corollary that training two-layer ReLU neural networks on orthogonally separable datasets can cause their adversarial reprogramming to fail. We support these theoretical results by experiments that demonstrate that, as long as batch normalisation layers are suitably initialised, even untrained networks with random weights are susceptible to adversarial reprogramming. This is in contrast to observations in several recent works that suggested that adversarial reprogramming is not possible for untrained networks to any degree of reliability.

Logical Limitations to Machine Ethics with Consequences to Lethal Autonomous Weapons

Lethal Autonomous Weapons promise to revolutionize warfare -- and raise a multitude of ethical and legal questions. It has thus been suggested to program values and principles of conduct (such as the Geneva Conventions) into the machines' control, thereby rendering them both physically and morally superior to human combatants. We employ mathematical logic and theoretical computer science to explore fundamental limitations to the moral behaviour of intelligent machines in a series of "Gedankenexperiments": Refining and sharpening variants of the Trolley Problem leads us to construct an (admittedly artificial but) fully deterministic situation where a robot is presented with two choices: one morally clearly preferable over the other -- yet, based on the undecidability of the Halting problem, it provably cannot decide algorithmically which one. Our considerations have surprising implications to the question of responsibility and liability for an autonomous system's actions and lead to specific technical recommendations.