A Nonparametric Bayesian Approach to Uncovering Rat Hippocampal Population Codes During Spatial Navigation

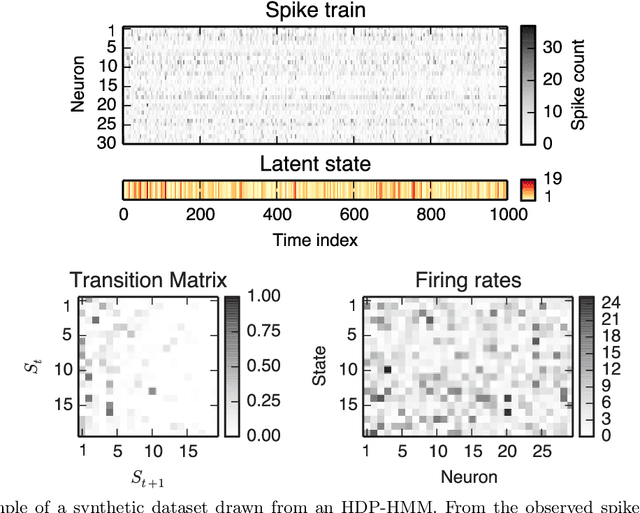
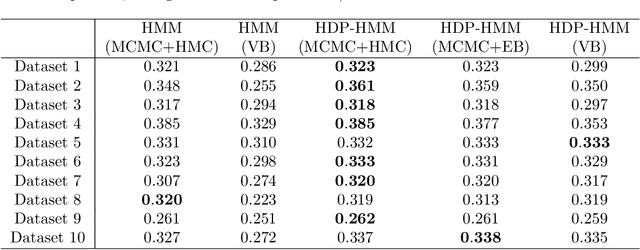
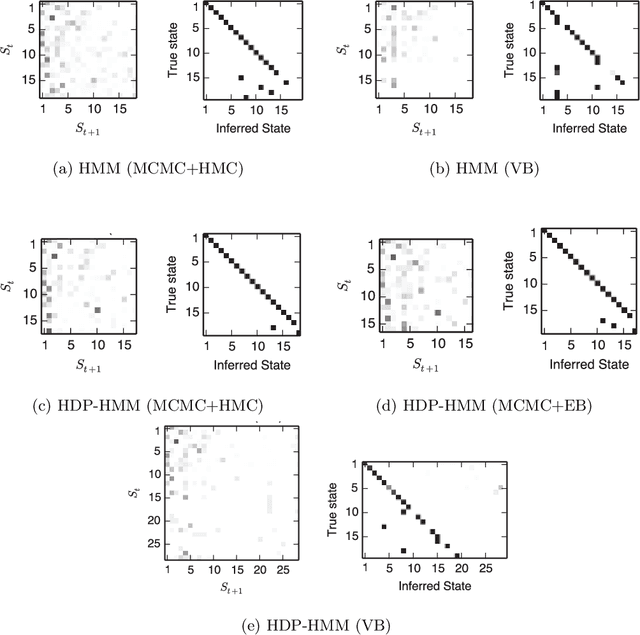
Rodent hippocampal population codes represent important spatial information about the environment during navigation. Several computational methods have been developed to uncover the neural representation of spatial topology embedded in rodent hippocampal ensemble spike activity. Here we extend our previous work and propose a nonparametric Bayesian approach to infer rat hippocampal population codes during spatial navigation. To tackle the model selection problem, we leverage a nonparametric Bayesian model. Specifically, to analyze rat hippocampal ensemble spiking activity, we apply a hierarchical Dirichlet process-hidden Markov model (HDP-HMM) using two Bayesian inference methods, one based on Markov chain Monte Carlo (MCMC) and the other based on variational Bayes (VB). We demonstrate the effectiveness of our Bayesian approaches on recordings from a freely-behaving rat navigating in an open field environment. We find that MCMC-based inference with Hamiltonian Monte Carlo (HMC) hyperparameter sampling is flexible and efficient, and outperforms VB and MCMC approaches with hyperparameters set by empirical Bayes.

Bayesian Nonparametric Hidden Semi-Markov Models

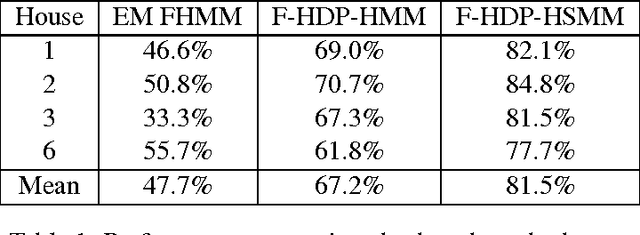
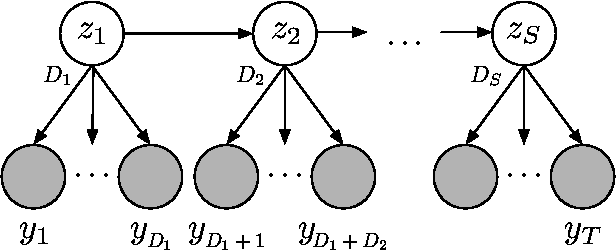
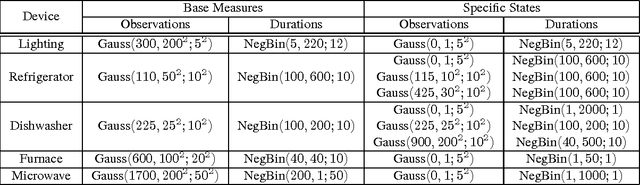
There is much interest in the Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) as a natural Bayesian nonparametric extension of the ubiquitous Hidden Markov Model for learning from sequential and time-series data. However, in many settings the HDP-HMM's strict Markovian constraints are undesirable, particularly if we wish to learn or encode non-geometric state durations. We can extend the HDP-HMM to capture such structure by drawing upon explicit-duration semi-Markovianity, which has been developed mainly in the parametric frequentist setting, to allow construction of highly interpretable models that admit natural prior information on state durations. In this paper we introduce the explicit-duration Hierarchical Dirichlet Process Hidden semi-Markov Model (HDP-HSMM) and develop sampling algorithms for efficient posterior inference. The methods we introduce also provide new methods for sampling inference in the finite Bayesian HSMM. Our modular Gibbs sampling methods can be embedded in samplers for larger hierarchical Bayesian models, adding semi-Markov chain modeling as another tool in the Bayesian inference toolbox. We demonstrate the utility of the HDP-HSMM and our inference methods on both synthetic and real experiments.

The Hierarchical Dirichlet Process Hidden Semi-Markov Model

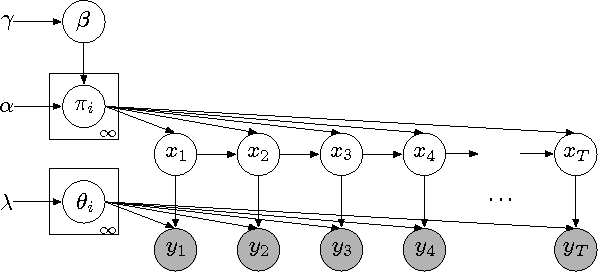
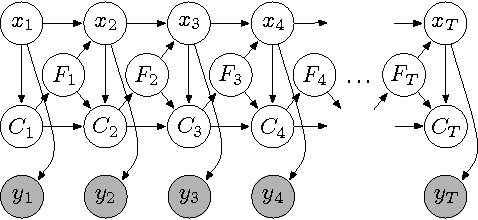
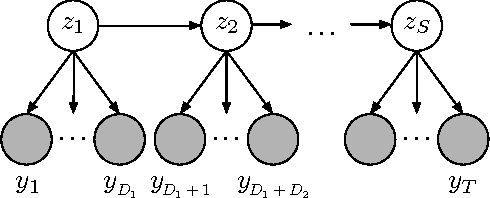
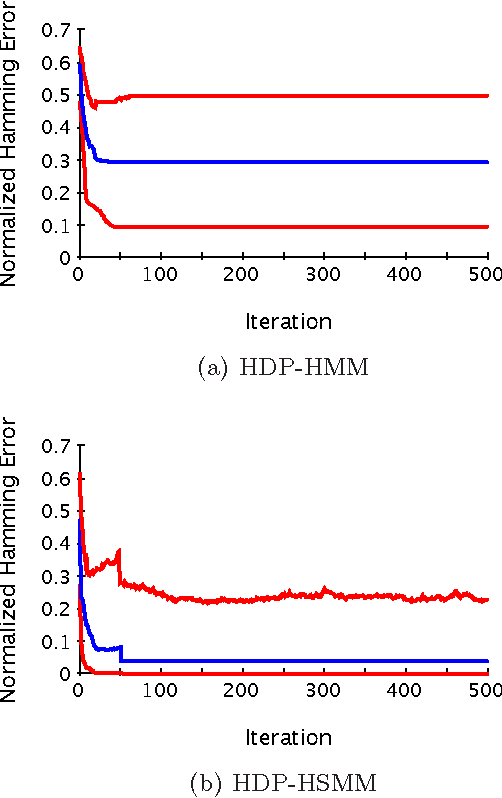
There is much interest in the Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) as a natural Bayesian nonparametric extension of the traditional HMM. However, in many settings the HDP-HMM's strict Markovian constraints are undesirable, particularly if we wish to learn or encode non-geometric state durations. We can extend the HDP-HMM to capture such structure by drawing upon explicit-duration semi-Markovianity, which has been developed in the parametric setting to allow construction of highly interpretable models that admit natural prior information on state durations. In this paper we introduce the explicitduration HDP-HSMM and develop posterior sampling algorithms for efficient inference in both the direct-assignment and weak-limit approximation settings. We demonstrate the utility of the model and our inference methods on synthetic data as well as experiments on a speaker diarization problem and an example of learning the patterns in Morse code.