Higher-order topological kernels via quantum computation

Topological data analysis (TDA) has emerged as a powerful tool for extracting meaningful insights from complex data. TDA enhances the analysis of objects by embedding them into a simplicial complex and extracting useful global properties such as the Betti numbers, i.e. the number of multidimensional holes, which can be used to define kernel methods that are easily integrated with existing machine-learning algorithms. These kernel methods have found broad applications, as they rely on powerful mathematical frameworks which provide theoretical guarantees on their performance. However, the computation of higher-dimensional Betti numbers can be prohibitively expensive on classical hardware, while quantum algorithms can approximate them in polynomial time in the instance size. In this work, we propose a quantum approach to defining topological kernels, which is based on constructing Betti curves, i.e. topological fingerprint of filtrations with increasing order. We exhibit a working prototype of our approach implemented on a noiseless simulator and show its robustness by means of some empirical results suggesting that topological approaches may offer an advantage in quantum machine learning.

The Quantum Path Kernel: a Generalized Quantum Neural Tangent Kernel for Deep Quantum Machine Learning

Building a quantum analog of classical deep neural networks represents a fundamental challenge in quantum computing. A key issue is how to address the inherent non-linearity of classical deep learning, a problem in the quantum domain due to the fact that the composition of an arbitrary number of quantum gates, consisting of a series of sequential unitary transformations, is intrinsically linear. This problem has been variously approached in the literature, principally via the introduction of measurements between layers of unitary transformations. In this paper, we introduce the Quantum Path Kernel, a formulation of quantum machine learning capable of replicating those aspects of deep machine learning typically associated with superior generalization performance in the classical domain, specifically, hierarchical feature learning. Our approach generalizes the notion of Quantum Neural Tangent Kernel, which has been used to study the dynamics of classical and quantum machine learning models. The Quantum Path Kernel exploits the parameter trajectory, i.e. the curve delineated by model parameters as they evolve during training, enabling the representation of differential layer-wise convergence behaviors, or the formation of hierarchical parametric dependencies, in terms of their manifestation in the gradient space of the predictor function. We evaluate our approach with respect to variants of the classification of Gaussian XOR mixtures - an artificial but emblematic problem that intrinsically requires multilevel learning in order to achieve optimal class separation.

Structure Learning of Quantum Embeddings

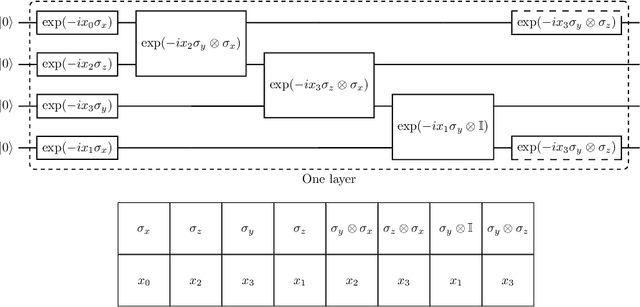
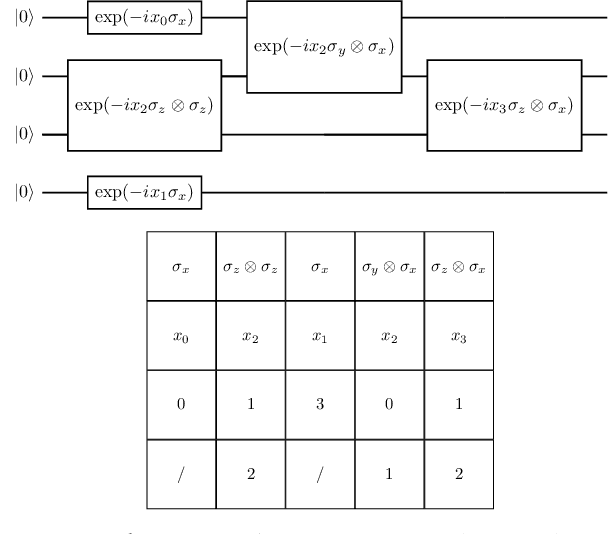
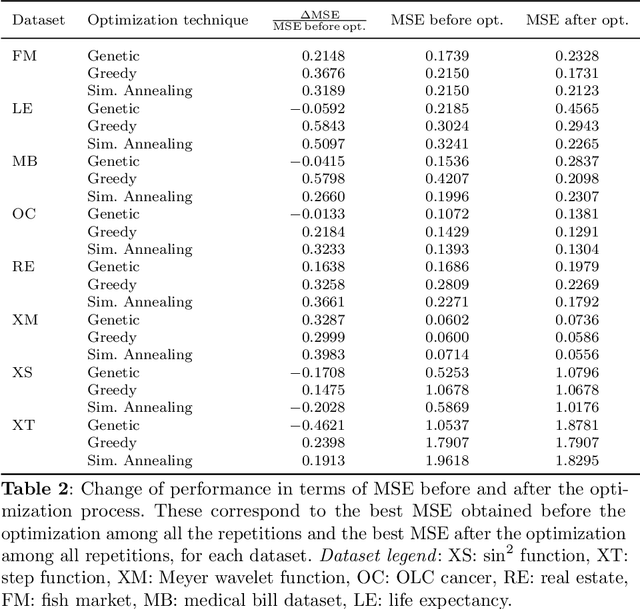
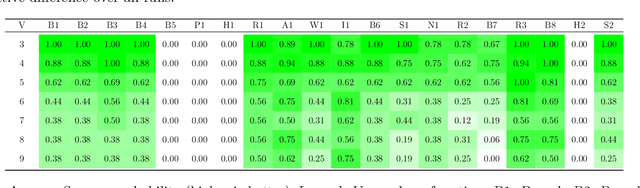
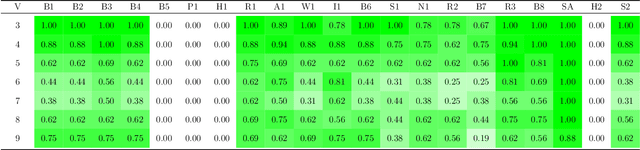
The representation of data is of paramount importance for machine learning methods. Kernel methods are used to enrich the feature representation, allowing better generalization. Quantum kernels implement efficiently complex transformation encoding classical data in the Hilbert space of a quantum system, resulting in even exponential speedup. However, we need prior knowledge of the data to choose an appropriate parametric quantum circuit that can be used as quantum embedding. We propose an algorithm that automatically selects the best quantum embedding through a combinatorial optimization procedure that modifies the structure of the circuit, changing the generators of the gates, their angles (which depend on the data points), and the qubits on which the various gates act. Since combinatorial optimization is computationally expensive, we have introduced a criterion based on the exponential concentration of kernel matrix coefficients around the mean to immediately discard an arbitrarily large portion of solutions that are believed to perform poorly. Contrary to the gradient-based optimization (e.g. trainable quantum kernels), our approach is not affected by the barren plateau by construction. We have used both artificial and real-world datasets to demonstrate the increased performance of our approach with respect to randomly generated PQC. We have also compared the effect of different optimization algorithms, including greedy local search, simulated annealing, and genetic algorithms, showing that the algorithm choice largely affects the result.

QuASK -- Quantum Advantage Seeker with Kernels

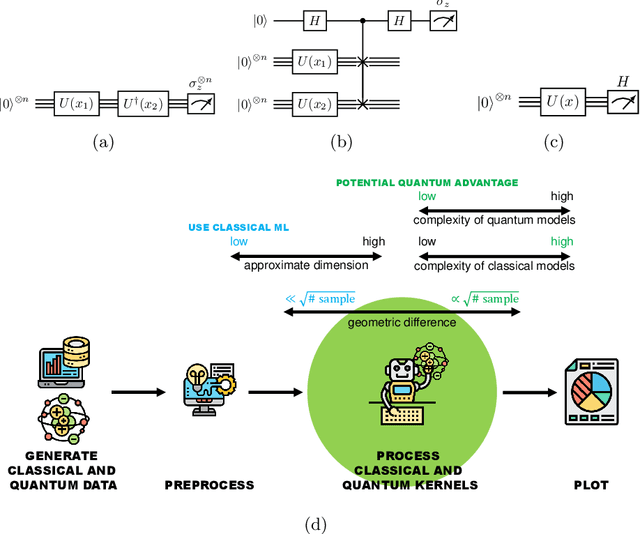
QuASK is a quantum machine learning software written in Python that supports researchers in designing, experimenting, and assessing different quantum and classical kernels performance. This software is package agnostic and can be integrated with all major quantum software packages (e.g. IBM Qiskit, Xanadu's Pennylane, Amazon Braket). QuASK guides the user through a simple preprocessing of input data, definition and calculation of quantum and classical kernels, either custom or pre-defined ones. From this evaluation the package provides an assessment about potential quantum advantage and prediction bounds on generalization error. Moreover, it allows for the generation of parametric quantum kernels that can be trained using gradient-descent-based optimization, grid search, or genetic algorithms. Projected quantum kernels, an effective solution to mitigate the curse of dimensionality induced by the exponential scaling dimension of large Hilbert spaces, are also calculated. QuASK can furthermore generate the observable values of a quantum model and use them to study the prediction capabilities of the quantum and classical kernels.

Benchmarking Small-Scale Quantum Devices on Computing Graph Edit Distance

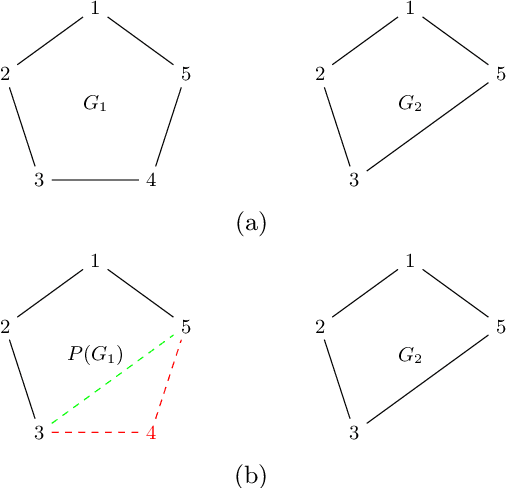
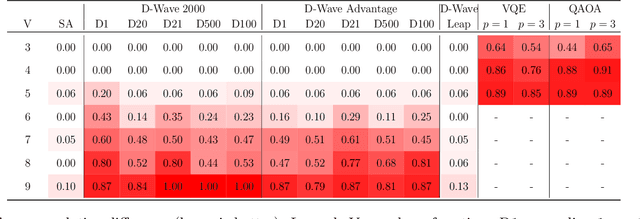
Distance measures provide the foundation for many popular algorithms in Machine Learning and Pattern Recognition. Different notions of distance can be used depending on the types of the data the algorithm is working on. For graph-shaped data, an important notion is the Graph Edit Distance (GED) that measures the degree of (dis)similarity between two graphs in terms of the operations needed to make them identical. As the complexity of computing GED is the same as NP-hard problems, it is reasonable to consider approximate solutions. In this paper we present a comparative study of two quantum approaches to computing GED: quantum annealing and variational quantum algorithms, which refer to the two types of quantum hardware currently available, namely quantum annealer and gate-based quantum computer, respectively. Considering the current state of noisy intermediate-scale quantum computers, we base our study on proof-of-principle tests of the performance of these quantum algorithms.

Facial Expression Recognition on a Quantum Computer

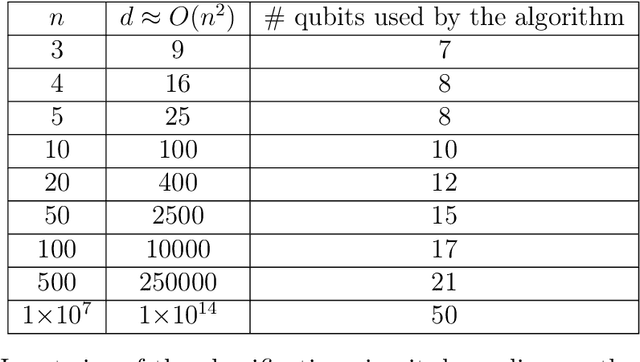
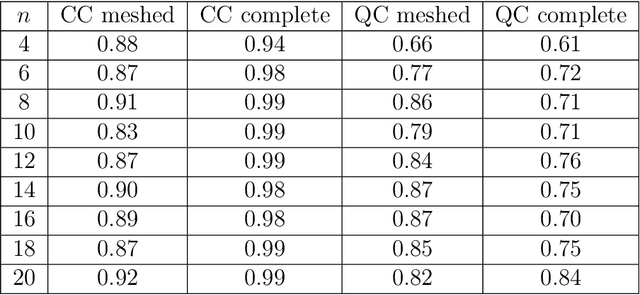
We address the problem of facial expression recognition and show a possible solution using a quantum machine learning approach. In order to define an efficient classifier for a given dataset, our approach substantially exploits quantum interference. By representing face expressions via graphs, we define a classifier as a quantum circuit that manipulates the graphs adjacency matrices encoded into the amplitudes of some appropriately defined quantum states. We discuss the accuracy of the quantum classifier evaluated on the quantum simulator available on the IBM Quantum Experience cloud platform, and compare it with the accuracy of one of the best classical classifier.